26 câu hỏi trắc nghiệm thuộc Dạng 2: Chứng minh phương trình có nghiệm có đáp án

Câu 1:

Chứng minh rằng phương trình $x^{2020} + 3 x^{5} - 1 = 0$ có nghiệm.

Xem đáp án

Hướng dẫn giải

Ta có hàm số $f (x) = x^{2020} + 3 x^{5} - 1$ liên tục trên R và $f (0) . f (1) = - 3 < 0$

Suy ra phương trình f(x) =0 có ít nhất một nghiệm thuộc (0,1)

Câu 2:

Chứng minh phương trình $x^{2} \sin x + x \cos x + 1 = 0$ có ít nhất một nghiệm.

Xem đáp án

Hướng dẫn giải

Ta có hàm số $f (x) = x^{2} \sin x + x \cos x + 1$ liên tục trên R và $f (0) . f (π) = - π + 1 < 0$

Suy ra phương trình $f (x) = 0$ có ít nhất một nghiệm thuộc $(0; π)$

Câu 3:

Chứng minh rằng phương trình $x^{3} + 2 x = 4 + 3 \sqrt{3 - 2 x}$ có đúng một nghiệm.

Xem đáp án

Hướng dẫn giải

Điều kiện xác định: $x \leq \frac{3}{2}$

Ta có $x^{3} + 2 x = 4 + 3 \sqrt{3 - 2 x} \Leftrightarrow x^{3} + 2 x - 3 \sqrt{3 - 2 x} - 4 = 0$

Xét hàm số $f (x) = x^{3} + 2 x - 3 \sqrt{3 - 2 x} - 4$ liên tục trên $(- \infty; \frac{3}{2}]$ và $f (0) = - 4 - 3 \sqrt{3} < 0, f (\frac{3}{2}) = \frac{19}{8} > 0 \Rightarrow f (0) . f (\frac{3}{2}) < 0$

Do đó phương trình f(x) =0 có ít nhất một nghiệm

Giả sử phương trình f(x)= 0 có hai nghiệm $x_{1}; x_{2}$

Khi đó $f (x_{1}) - f (x_{2}) = 0$

$\Leftrightarrow (x_{1}^{3} - x_{2}^{3}) + 2 (x_{1} - x_{2}) - 3 (\sqrt{3 - 2 x_{1}} - \sqrt{3 - 2 x_{2}}) = 0$

$\Leftrightarrow (x_{1} - x_{2}) \underset{B}{\underset{⏟}{(x_{1}^{2} + x_{1} x_{2} + x_{2}^{2} + 2 + \frac{6}{\sqrt{3 - 2 x_{1}} + \sqrt{3 - 2 x_{2}}})}} = 0$

$\Leftrightarrow x_{1} = x_{2}$ (vì $B = {(x_{1} + \frac{x_{2}}{2})}^{2} + \frac{3 x_{2}^{2}}{4} + 4 + \frac{6}{\sqrt{3 - 2 x_{1}} + \sqrt{3 - 2 x_{2}}} > 0$ )

Vậy phương trình có đúng một nghiệm.

Câu 4:

Chứng minh rằng phương trình

\sqrt{x^{5} + 2 x^{3} + 15 x^{2} + 14 x + 2} = 3 x^{2} + x + 1

có đúng năm nghiệm phân biệt.

Xem đáp án

Hướng dẫn giải

Phương trình đã cho tương đương với $x^{5} + 2 x^{3} + 15 x^{2} + 14 x + 2 = {(3 x^{2} + x + 1)}^{2}$

$\Leftrightarrow x^{5} - 9 x^{4} - 4 x^{3} + 18 x^{2} + 12 x + 1 = 0 (1)$

Xét hàm số $f (x) =^{5} - 9 x^{4} - 4 x^{3} + 18 x^{2} + 12 x + 1$ liên tục trên R

Ta có: $f (- 2) = - 95 < 0, f (- 1) = 1 > 0, f (- \frac{1}{2}) = - \frac{19}{32} < 0$

$f (0) = 1 > 0, f (2) = - 47, f (10) = 7921 > 0$

Do đó phương trình f(x) có ít nhất năm nghiệm thuộc các khoảng

$(- 2; - 1), (- 1; - \frac{1}{2}), (- \frac{1}{2}; 0), (0; 2), (2; 10)$

Mặt khác f(x) là đa thức bậc năm nên có tối đa năm nghiệm.

Vậy phương trình đã cho có đúng năm nghiệm.

Câu 5:

Tìm các giới hạn sau:

b, $\lim {(2 n + 1)}^{2} (\frac{3}{n^{2} + 2 n} - \frac{1}{n^{2} + 3 n - 1}) .$

Xem đáp án

$\lim {(2 n + 1)}^{2} (\frac{3}{n^{2} + 2 n} - \frac{1}{n^{2} + 3 n - 1})$

$= \lim \frac{3 {(2 n + 1)}^{2}}{n^{2} + 2 n} - \lim \frac{{(2 n + 1)}^{2}}{n^{2} + 3 n - 1} .$

Mà

$\lim \frac{3 {(2 n + 1)}^{2}}{n^{2} + 2 n} = \lim \frac{3 {(2 + \frac{1}{n})}^{2}}{1 + \frac{2}{n}} = \frac{{3.2}^{2}}{1} = 12.$

$\lim \frac{{(2 n + 1)}^{2}}{n^{2} + 3 n - 1} = \frac{{(2 + \frac{1}{n})}^{2}}{1 + \frac{3}{n} - \frac{1}{n^{2}}} = \frac{2^{2}}{1} = 4.$

Nên

$\lim {(2 n + 1)}^{2} (\frac{3}{n^{2} + 2 n} - \frac{1}{n^{2} + 3 n - 1}) = 12 - 4 = 8.$

Câu 6:

Tìm các giới hạn sau:

a)

\lim \frac{\sqrt{9 n^{2} + 2 n} - 3 n}{4 n + 3} .

Xem đáp án

a, $\lim \frac{\sqrt{9 n^{2} + 2 n} - 3 n}{4 n + 3} = \lim \frac{n \sqrt{9 + \frac{2}{n^{2}}} - 3 n}{4 n + 3} = \lim \frac{\sqrt{9 + \frac{2}{n^{2}}} - 3}{4 + \frac{3}{n}} = \frac{\sqrt{9 + 0} - 3}{4 + 0} = \frac{0}{4} = 0.$

Câu 7:

Tìm các giới hạn sau: b,

\lim \frac{3 \sqrt[4]{n^{5}} + 4 n - 2}{2 \sqrt[4]{n^{5}} - 3 n} .

Xem đáp án

b, $\lim \frac{3 \sqrt[4]{n^{5}} + 4 n - 2}{2 \sqrt[4]{n^{5}} - 3 n} = \lim \frac{3 + \frac{4}{\sqrt[4]{n}} - \frac{2}{\sqrt[4]{n^{5}}}}{2 - \frac{3}{\sqrt[4]{n}}} = \frac{3 + 0 - 0}{2 - 0} = \frac{3}{2} .$

Câu 8:

Tìm các giới hạn sau: $\lim (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n^{2} + n^{3}}) .$

Xem đáp án

$\lim (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n^{2} + n^{3}}) = \lim (\sqrt{n^{2} + 2 n + 3} - n) + \lim (n - \sqrt[3]{n^{2} + n^{3}}) .$

Mà

$\lim (\sqrt{n^{2} + 2 n + 3} - n) = \lim \frac{n^{2} + 2 n + 3 - n^{2}}{\sqrt{n^{2} + 2 n + 3} + n} = \lim \frac{2 + \frac{3}{n}}{\sqrt{1 + \frac{2}{n} + \frac{3}{n^{2}}} + 1} = \frac{2}{1 + 1} = 1.$

$\lim (n - \sqrt[3]{n^{2} + n^{3}}) = \lim \frac{n^{3} - (n^{2} + n^{3})}{n^{2} + n . \sqrt[3]{n^{2} + n^{3}} + {(\sqrt[3]{n^{2} + n^{3}})}^{2}}$

$= \lim \frac{- 1}{1 + \sqrt[3]{\frac{1}{n} + 1} + {(\sqrt[3]{\frac{1}{n} + 1})}^{2}} = \frac{- 1}{1 + 1 + 1} = - \frac{1}{3} .$

Vậy $\lim (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n^{2} + n^{3}}) = 1 - \frac{1}{3} = \frac{2}{3} .$

Câu 9:

Tìm các giới hạn sau:

a)

\lim (\sqrt{4 n^{2} + 2 n} - 2 n) .

Xem đáp án

a) $\lim (\sqrt{4 n^{2} + 2 n} - 2 n) = \lim \frac{4 n^{2} + 2 n - 4 n^{2}}{\sqrt{4 n^{2} + 2 n} + 2 n} = \lim \frac{2 n}{2 n (\sqrt{1 + \frac{1}{2 n}} + 1)}$

= \lim \frac{1}{\sqrt{1 + \frac{1}{2 n}} + 1} = \frac{1}{\sqrt{1 + 0} + 1} = \frac{1}{2} .

Câu 10:

Tìm các giới hạn sau:

a)

\lim \frac{3^{n} - {2.5}^{n}}{7 + {3.5}^{n}} .

Xem đáp án

a, $\lim \frac{3^{n} - {2.5}^{n}}{7 + {3.5}^{n}} = \lim \frac{{(\frac{3}{5})}^{n} - 2}{7. {(\frac{1}{5})}^{n} + 3} = \frac{0 - 2}{7.0 + 3} = - \frac{2}{3}$

Câu 11:

Tìm các giới hạn sau: b, $\lim \frac{1 + 2 + 2^{2} + ... + 2^{n}}{1 + 3 + 3^{2} + ... + 3^{n}} .$

Xem đáp án

b, $\lim \frac{1 + 2 + 2^{2} + ... + 2^{n}}{1 + 3 + 3^{2} + ... + 3^{n}} = \lim \frac{2^{n + 1} - 1}{\frac{3^{n + 1} - 1}{2}} = \lim 2. \frac{{(\frac{2}{3})}^{n + 1} - {(\frac{1}{3})}^{n + 1}}{1 - {(\frac{1}{3})}^{n + 1}} = 0.$

Câu 12:

Tìm các giới hạn sau:

a) $\lim (\frac{1}{1.3} + \frac{1}{3.5} + ... + \frac{1}{(2 n - 1) (2 n + 1)}) .$

Xem đáp án

Hướng dẫn giải

a) Do

\frac{1}{(2 k - 1) (2 k + 1)} = \frac{1}{2} . \frac{2 k + 1 - (2 k - 1)}{(2 k - 1) (2 k + 1)} = \frac{1}{2} (\frac{1}{2 k - 1} - \frac{1}{2 k + 1})

Suy ra $\lim (\frac{1}{1.3} + \frac{1}{3.5} + ... + \frac{1}{(2 k - 1) (2 k + 1)})$

$= \lim \frac{1}{2} (\frac{1}{1} - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + ... + \frac{1}{2 n - 1} - \frac{1}{2 n + 1}) = \lim \frac{1}{2} (1 - \frac{1}{2 n + 1}) = \frac{1}{2} .$

Câu 13:

Tìm các giới hạn sau: b, $\lim (1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) ... (1 - \frac{1}{n^{2}}) .$

Xem đáp án

b) Ta có $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ... (1 - \frac{1}{{(n - 1)}^{2}}) (1 - \frac{1}{n^{2}})$

$= \frac{1}{2} . \frac{3}{2} . \frac{2}{3} . \frac{4}{3} . \frac{3}{4} . \frac{5}{4} ... \frac{n - 2}{n - 1} . \frac{n}{n - 1} . \frac{n - 1}{n} . \frac{n + 1}{n} = \frac{n + 1}{2 n} .$

Suy ra $\lim (1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) ... (1 - \frac{1}{n^{2}}) = \lim \frac{n + 1}{2 n} = \lim \frac{1 + \frac{1}{n}}{2} = \frac{1}{2} .$

Câu 14:

Tính các tổng sau:

a) $S = \frac{1}{3} + \frac{1}{3^{2}} + ... + \frac{1}{3^{n}} + ...$

Xem đáp án

Tính các tổng sau:

a) $S = \frac{1}{3} + \frac{1}{3^{2}} + ... + \frac{1}{3^{n}} + ...$

Câu 15:

Tính các tổng sau: b,

S = 16 - 8 + 4 - 2 + ...

Xem đáp án

b) Xét dãy số $u_{1} = 16, q = - \frac{1}{2} .$ là một cấp số nhân có $u_{1} = 16, q = - \frac{1}{2} .$

Suy ra

S = 16 - 8 + 4 - 2 + ...

có

\lim S = \frac{16}{1 + \frac{1}{2}} = \frac{32}{3} .

Câu 16:

Hãy biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:

α = 0, 353535...

Xem đáp án

Hướng dẫn giải

a) $α = 0, 353535... = 0, 35 + 0, 0035 + ... = \frac{35}{10^{2}} + \frac{35}{10^{4}} + ... = \frac{\frac{35}{10^{2}}}{1 - \frac{1}{10^{2}}} = \frac{35}{99} .$

Câu 17:

Hãy biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số: b,

β = 5, 231231...

Xem đáp án

b) $β = 5, 231231... = 5 + 0, 231 + 0, 000231 + ... = 5 + \frac{231}{10^{3}} + \frac{231}{10^{6}} + ...$

$= 5 + \frac{\frac{231}{10^{3}}}{1 - \frac{1}{10^{3}}} = 5 + \frac{231}{999} = \frac{1742}{333} .$

Câu 18:

Tính giới hạn sau: $\lim \frac{n^{2} + 4 n}{n^{2} + 4 n + 5} .$

Xem đáp án

Hướng dẫn giải

Nhập vào máy tính biểu thức sau:

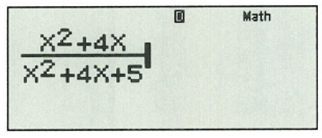
Tính giới hạn sau: lim n^2 +4x / n^2 +4n +5 (ảnh 1)

Sau đó bấm CALC.

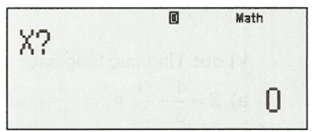
Tính giới hạn sau: lim n^2 +4x / n^2 +4n +5 (ảnh 2)

Nhập $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

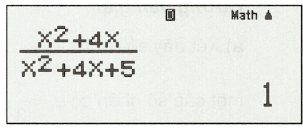
Tính giới hạn sau: lim n^2 +4x / n^2 +4n +5 (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng 1

Câu 19:

Tính giới hạn sau

\lim (\sqrt{4 n^{2} - 5 n} - 2 n) .

Xem đáp án

Hướng dẫn giải

Nhập vào máy tính biểu thức sau:

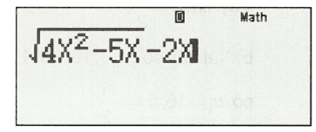
Tính giới hạn sau lim căn 4n^2 -5n -2n (ảnh 1)

Sau đó bấm CACL.

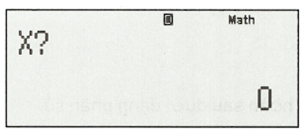
Tính giới hạn sau lim căn 4n^2 -5n -2n (ảnh 2)

Nhập: $x = 9999999999$ sau đó bấm “=”, ta được kết quả:

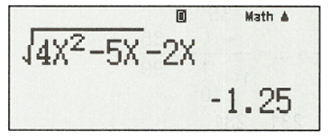
Tính giới hạn sau lim căn 4n^2 -5n -2n (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng $- 1, 25 = - \frac{5}{4} .$

Câu 20:

Cho hàm số f(x) xác định trên . Khẳng định nào sau đây đúng?

A. Nếu hàm số f(x) liên tục trên $[a, b]$ và $f (a) f (b) > 0$ thì phương trình không có nghiệm trong khoảng (a,b)

B. Nếu

f (a) f (b) < 0

thì phương trình f(x) =0 có ít nhất một nghiệm trong khoảng (a,b)

C. Nếu hàm số f(x) liên tục, tăng trên

[a, b]

và

f (a) f (b) > 0

thì phương trình không có nghiệm trong khoảng (a,b)

D. Nếu phương trình fx) =0 có nghiệm trong khoảng (a,b) thì hàm số f(x) phải liên tục trên (a, b)

Xem đáp án

Vì

f (a) f (b) > 0

nên f(a) và f(b) cùng dương hoặc cùng âm. Mà f(x) liên tục, tăng trên

[a; b]

nên đồ thị hàm f(x) nằm trên hoặc nằm dưới trục hoành trên

[a; b]

. Vậy phương trình f(x) =0 không có nghiệm trong khoảng (a,b)

Câu 21:

Trong các khẳng định sau

(I) f(x) liên tục trên đoạn $[a; b]$ và $f (a) . f (b) < 0$ thì phương trình f(x)=0 có nghiệm

(II) f(x) không liên tục trên $[a, b]$ và $f (a) . f (b) \geq 0$ thì phương trìnhf(x)=0 vô nghiệm

(III) f(x) liên tục trên đoạn $[a, b]$ và $f (a) . f (b) > 0$ thì tồn tại ít nhất một số $c \in (a; b)$ sao cho $f (c) = 0$

(IV) f(x) liên tục trên đoạn $[a, b]$ và $f (a) . f (b) < 0$ thì tồn tại ít nhất một số $c \in (a; b)$ sao cho $f (c) = 0$

Số khẳng định đúng là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn đáp án B

Câu 22:

Cho phương trình $2 x^{4} - 5 x^{2} + x + 1 = 0$ . Khẳng định nào sau đây đúng?

A. Phương trình đã cho không có nghiệm trong khoảng $(- 1; 1)$

B. Phương trình đã cho chỉ có một nghiệm trong khoảng $(- 2; 1)$

C. Phương trình đã cho có ít nhất một nghiệm trong khoảng $(0 : 2)$

D. Phương trình đã cho không có nghiệm trong khoảng $(- 2; 0)$

A. Phương trình đã cho không có nghiệm trong khoảng $(- 1; 1)$

B. Phương trình đã cho chỉ có một nghiệm trong khoảng $(- 2; 1)$

C. Phương trình đã cho có ít nhất một nghiệm trong khoảng $(0 : 2)$

D. Phương trình đã cho không có nghiệm trong khoảng

(- 2; 0)

Xem đáp án

Đặt $f (x) = 2 x^{4} - 5 x^{2} + x + 1$ , hàm số $f (x)$ liên tục trên $(0; 2)$

Ta có $f (0) = 1; f (1) = - 1 \Rightarrow f (0) . f (1) < 0$ nên phương trình đã cho có ít nhất một nghiệm trong khoảng $(0; 2)$

Câu 23:

Tìm các giá trị của tham số m sao cho phương trình $x^{3} - 3 x^{2} + (2 m - 2) x + m - 3 = 0$ có ba nghiệm $x_{1}, x_{2}, x_{3}$ thỏa mãn $x_{1} < - 1 < x_{2} < x_{3}$

A. $m > - 5$

B. $m < - 5$

C. $m \leq - 5$

D. $m < - 6$

Xem đáp án

Đặt $f (x) = x^{3} - 3 x^{2} + (2 m - 2) x + m - 3$ . Ta thấy hàm số liên tục trên R

Điều kiện cần: $a f (- 1) > 0 \Leftrightarrow - m - 5 > 0 \Leftrightarrow m < - 5$

Điều kiện đủ: với $m < - 5$ ta có

+) $\lim_{x \to - \infty} f (x) = - \infty$ nên tồn tại $a < - 1$ sao cho $f (a) < 0$

Mặt khác $f (- 1) = - m - 5 > 0$ . Suy ra $f (a) . f (- 1) < 0$

Do đó tồn tại $x_{1} \in (a; - 1)$ sao cho $f (x_{1}) = 0$

+) $f (0) = m - 3 < 0, f (- 1) > 0$ . Suy ra $f (0) . f (- 1) < 0$

Do đó tồn tại $x_{2} \in (- 1; 0)$ sao cho $f (x_{2}) = 0$

+) $\lim_{x \to + \infty} f (x) = + \infty$ nên tồn tại $b > 0$ sao cho $f (b) > 0$

Mặt khác $f (0) < 0$ . Suy ra $f (0) . f (b) < 0$

Do đó tồn tại $x_{3} \in (0; b)$ sao cho $f (x_{3}) = 0$ . Vậy $m < - 5$ thỏa mãn yêu cầu bài toán

Câu 24:

Cho các số thực a, b, c thỏa mãn $4 a + c > 8 + 2 b$ và $a + b + c < - 1$ . Khi đó số nghiệm thực phân biệt của phương trình $x^{3} + a x^{2} + b x + c = 0$ bằng

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Xét phương trình: $x^{3} + a x^{2} + b x + c = 0 (1)$

Đặt: $f (x) = x^{3} + a x^{2} + b x + c$

Từ giả thiết $\{\begin{cases} 4 a + c > 8 + 2 b \Rightarrow - 8 + 4 a - 2 b + c > 0 \\ a + b + c < - 1 \Rightarrow 1 a + b + c < 0 \Rightarrow f (1) < 0 \end{cases}$

Do đó $f (- 2) . f (1) < 0$ nên phương trình (1) có ít nhất một nghiệm trong $(- 2; 1)$

Ta nhận thấy:

$\lim_{x \to - \infty} f (x) = - \infty$ mà $f (- 2) > 0$ nên phương trình (1) có ít nhất một nghiệm $α \in (- \infty; - 2)$

Tương tự: $\lim_{x \to + \infty} f (x) = + \infty$ mà $f (1) < 0$ nên phương trình (1) có ít nhất một nghiệm $β \in (1; + \infty)$

Như vậy phương trình đã cho có ít nhất 3 nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa 3 nghiệm.

Câu 25:

Cho phương trình $x^{3} + a x^{2} + b x + c = 0$ (1) trong đó a, b, c là các tham số thực. Chọn khẳng định đúng trong các khẳng định sau

A. Phương trình (1) vô nghiệm với mọi a, b, c

B. Phương trình (1) có ít nhất một nghiệm với mọi a, b, c

C. Phương trình (1) có ít nhất hai nghiệm với mọi a, b, c

D. Phương trình (1) có đúng ba nghiệm phân biệt với mọi a, b, c

A. Phương trình (1) vô nghiệm với mọi a, b, c

B. Phương trình (1) có ít nhất một nghiệm với mọi a, b, c

C. Phương trình (1) có ít nhất hai nghiệm với mọi a, b, c

D. Phương trình (1) có đúng ba nghiệm phân biệt với mọi a, b, c

Xem đáp án

Xét hàm số $f (x) = x^{3} + a x^{2} + b x + c$ liên tục trên R

$\lim_{x \to - \infty} f (x) = - \infty; \lim_{x \to + \infty} f (x) = + \infty$ nên sẽ tồn tại số $α \to - \infty$ và sao cho $f (α) . f (β) < 0$

Vậy phương trình (1) có ít nhất một nghiệm với mọi a, b, c.

Ta lại có với $a = b = 0; c = 1$ thì phương trình có đúng một nghiệm thực

Câu 26:

Tìm giá trị của tham số m để phương trình $(m^{2} - 5 x + 6) {(x + 5)}^{2019} (x^{2020} + 2 x) + 2 x - 1 = 0$ có nghiệm

A. $m \in \{2; 3\}$

B. $m \in ℝ \ \{2; 3\}$

C. $m \in \emptyset$

D. $m \in ℝ$

Xem đáp án

Bổ đề: Phương trình đa thức bậc lẻ $a_{2 n + 1} x^{2 n + 1} + a_{2 n} x^{2 n} + ... + a_{1} x + a_{0} = 0$ luôn có ít nhất một nghiệm, với mọi giá trị của $a_{i}, i = \bar{2 n + 1, 0}$

Chứng minh:

+ Xét hàm số $f (x) = a_{2 n + 1} x^{2 n + 1} + a_{2 n} x^{2 n} + ... + a_{1} x + a_{0}$ đây là hàm đa thức, xác định trên R nên liên tục trên R

Ta có: $\lim_{x \to + \infty} f (x) = \lim_{x \to + \infty} [a_{2 n + 1} x^{2 n + 1} + a_{2 n} x^{2 n} + ... + a_{1} x + a_{0}] = + \infty$ nên tồn tại $x_{1} \in ℝ$ sao cho $f (x_{1}) > 0$

$\lim_{x \to - \infty} f (x) = \lim_{x \to + \infty} [a_{2 n + 1} x^{2 n + 1} + a_{2 n} x^{2 n} + ... + a_{1} x + a_{0}] = - \infty$ nên tồn tại $x_{2} \in ℝ$ sao cho $f (x_{2}) < 0$

Do đó tồn tại $x_{0} \in (x_{1}; x_{2})$ sao cho $f (x_{0}) = 0$

Vậy phương trình đa thức bậc lẻ luôn có ít nhất một nghiệm, với mọi giá trị của $a_{i}, i = \bar{2 n + 1, 0}$

Áp dụng:

Đặt $f (x) = (m^{2} - 5 x + 6) {(x + 5)}^{2019} (x^{2020} + 2 x) + 2 x - 1$ Hàm số f(x) liên tục trên R

+ Xét $m^{2} - 5 m + 6 \Leftrightarrow [\begin{array}{l} m = 2 \\ m = 3 \end{array}$ . Khi đó phương trình trở thành $2 x - 1 = 0 \Leftrightarrow x = \frac{1}{2}$

+ Xét $m^{2} - 5 m + 6 \neq 0 \Rightarrow \{\begin{cases} m \neq 2 \\ m \neq 3 \end{cases}$ .

Hàm f(x) có bậc cao nhất là $2019 + 2020 = 4039$ là đa thức bậc lẻ nên f(x)=0 có ít nhất một nghiệm với $\forall m \in ℝ$

Bài tập chuyên đề toán 11 Bài 3: Hàm số liên tục có đáp án

Dạng 2: Chứng minh phương trình có nghiệm có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương