Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều

Bài 4 trang 78 Toán 7 Tập 2:

Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.

Trả lời

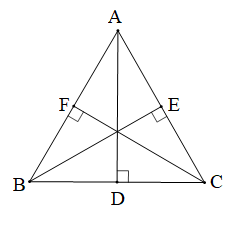
• Xét ∆FBC (vuông tại F) và ∆ECB (vuông tại E) có:

CF = BE (giả thiết);

BC là cạnh chung.

Do đó ∆FBC = ∆ECB (cạnh huyền - cạnh góc vuông).

Suy ra $\widehat{FBC}=\widehat{ECB}$ (hai góc tương ứng).

Hay $\widehat{ABC}=\widehat{ACB}$ 

Khi đó tam giác ABC cân tại A.

Suy ra AB = AC (1).

• Tương tự ta cũng có ∆ABD = ∆BAE (cạnh huyền - cạnh góc vuông).

Suy ra $\widehat{\text{ABD}}=\widehat{BAE}$ (hai góc tương ứng).

Hay $\widehat{ABC}=\widehat{BAC}$ do đó tam giác ABC cân tại C.

Suy ra CA = CB (2).

Từ (1) và (2) ta có AB = BC = CA

Do đó tam giác ABC đều.

Vậy tam giác ABC đều.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học

Bài tập cuối chương 8