Giải SGK Toán 7 Bài 3 (Cánh diều): Hai tam giác bằng nhau
A. Câu hỏi trong bài
Giải Toán 7 trang 78 Tập 2
Lời giải
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
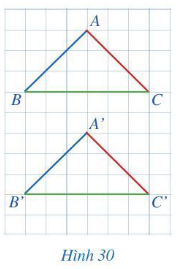
Khi hai tam giác có thể chồng khít lên nhau tức là hai tam giác bằng nhau.
Giả sử hai tam giác đó là ∆ABC và ∆A'B'C'.
Ta có: ∆ABC = ∆A'B'C'
Suy ra:
+) AB = A'B'; BC = B'C'; CA = C'A';
+) ˆA=A'
Vậy khi hai tam giác có thể chồng khít lên nhau thì các cạnh và các góc tương ứng của hai tam giác bằng nhau.
Sau khi đặt tam giác ABC chồng khít lên tam giác A'B'C', hãy so sánh:
a) Các cạnh tương ứng: AB và A'B'; BC và B'C'; CA và C'A';
b) Các góc tương ứng: và ; và , và
Lời giải
Sau khi đặt tam giác ABC chồng khít lên tam giác A'B'C' ta thấy:
a) AB = A'B'; BC = B'C'; CA = C'A';
b)
Giải Toán 7 trang 79 Tập 2
– Các cặp cạnh: AB và A'B'; BC và B'C'; CA và C'A'.
b) Hai tam giác ABC và A'B'C' có bằng nhau hay không?
Lời giải
Ta coi cạnh của hình ô vuông nhỏ là 1 đơn vị.
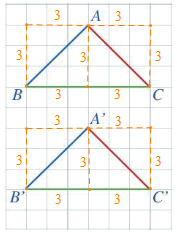
Khi đó cạnh AB là đường chéo của hình vuông có cạnh bằng 3 đơn vị;
Tương tự:
+ Cạnh A'B' là đường chéo của hình vuông có cạnh bằng 3 đơn vị;
+ Cạnh AC là đường chéo của hình vuông có cạnh bằng 3 đơn vị;
+ Cạnh A'C' là đường chéo của hình vuông có cạnh bằng 3 đơn vị;
+ Cạnh BC có độ dài bằng 6 đơn vị;
+ Cạnh B'C' có độ dài bànge 6 đơn vị.
a) Do đó ta có: AB = A'B'; BC = B'C'; CA = C'A';
Sử dụng thước đo góc ta đo được
b) Xét tam giác ABC và tam giác A'B'C' ta có:
+) AB = A'B'; BC = B'C'; CA = C'A';
+)
Do đó ∆ABC = ∆A'B'C'.
c) Ta có thể đặt mảnh giấy hình tam giác ABC chồng khít lên mảnh giấy hình tam giác A'B'C'.
Lời giải
|
GT |
∆ABC = ∆MNP, AC = 4 cm, |
|
KL |
Tính MP và |
Vì ∆ABC = ∆MNP (giả thiết) nên ta có:
+) AC = MP (hai cạnh tương ứng) mà AC = 4 cm nên MP = 4 cm;
+) (hai góc tương ứng) mà nên
Vậy MP = 4 cm và
B. Bài tập
Cho biết ∆ABC = ∆DEG, AB = 3 cm, BC = 4 cm, CA = 6 cm. Tìm độ dài các cạnh của tam giác DEG.
Lời giải
|
GT |
∆ABC = ∆DEG AB = 3 cm, BC = 4 cm, CA = 6 cm |
|
KL |
Tính DE, EF, DF |
Chứng minh (Hình vẽ dưới đây):
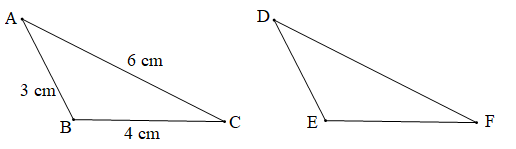
Vì ∆ABC = ∆DEG (giả thiết) nên ta có:
AB = DE; BC = EG; CA = GD (các cặp cạnh tương ứng)
Mà AB = 3 cm, BC = 4 cm, CA = 6 cm
Nên DE = 3 cm, EG = 4 cm, GD = 6 cm.
Vậy độ dài ba cạnh của tam giác DEG là: DE = 3 cm, EG = 4 cm, GD = 6 cm.
Cho biết ∆PQR = ∆IHK, Tính số đo góc K của tam giác IHK.
Lời giải
|
GT |
∆PQR = ∆IHK,
|
|
KL |
Tính |
Chứng minh (Hình vẽ dưới đây):
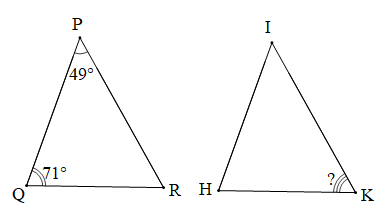
Xét tam giác PQR có: (tổng ba góc trong một tam giác)
Suy ra
Mà (giả thiết)
Do đó
Vì ∆PQR = ∆IHK (giả thiết) nên ta có: (hai góc tương ứng)
Mà
Do đó
Vậy số đo góc K của tam giác IHK bằng 60°.
Cho ∆ABC = ∆MNP và Tính số đo góc P.
Lời giải
|
GT |
∆ABC = ∆MNP,
|
|
KL |
Tính |
Chứng minh (Hình vẽ dưới đây)
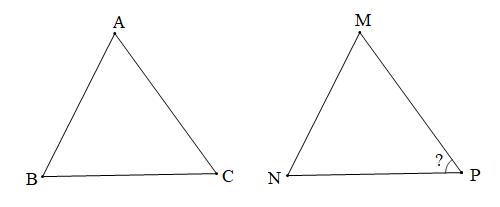
Vì ∆ABC = ∆MNP (giả thiết) nên ta có: (các cặp góc tương ứng)
Mà (giả thiết)
Suy ra
Xét tam giác MNP có: (tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo góc P của tam giác MNP bằng 55°.
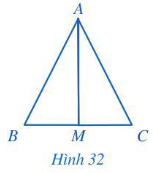
a) M là trung điểm của đoạn thẳng BC;
b) Tia AM là tia phân giác của góc BAC và
Lời giải
|
GT |
DABC, M ∈ BC ∆AMB = ∆AMC. |
|
KL |
a) M là trung điểm của BC; b) Tia AM là tia phân giác của góc BAC và |
Chứng minh (Hình 32):
a) Vì ∆AMB = ∆AMC (giả thiết) nên ta có: MB = MC (hai cạnh tương ứng)![]()
Suy ra M là trung điểm của BC.
b) Vì ∆AMB = ∆AMC (giả thiết) nên ta có:
+) (hai góc tương ứng) do đó tia AM là tia phân giác của góc BAC;
+) (hai góc tương ứng)
Lại có và là hai góc kề bù nên: (tính chất hai góc kề bù)
Suy ra
Hay
Do đó
Suy ra
Vậy tia AM là tia phân giác của góc BAC và
Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 1: Tổng các góc của một tam giác
Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc