Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC. Chứng minh rằng: M là trung điểm của đoạn thẳng BC
768
15/11/2023
Bài 4 trang 79 Toán 7 Tập 2: Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 32).
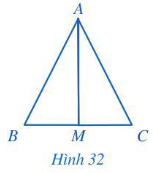
Chứng minh rằng:
a) M là trung điểm của đoạn thẳng BC;
b) Tia AM là tia phân giác của góc BAC và AM⊥BC.
Trả lời
|
GT
|
DABC, M ∈ BC
∆AMB = ∆AMC.
|
|
KL
|
a) M là trung điểm của BC;
b) Tia AM là tia phân giác của góc BAC và AM⊥BC.
|
Chứng minh (Hình 32):
a) Vì ∆AMB = ∆AMC (giả thiết) nên ta có: MB = MC (hai cạnh tương ứng)
Suy ra M là trung điểm của BC.
b) Vì ∆AMB = ∆AMC (giả thiết) nên ta có:
+) ^BAM=^CAM (hai góc tương ứng) do đó tia AM là tia phân giác của góc BAC;
+) ^AMB=^AMC (hai góc tương ứng)
Lại có ^AMB và ^AMC là hai góc kề bù nên: ^AMB+^AMC=180° (tính chất hai góc kề bù)
Suy ra
Hay
Do đó
Suy ra
Vậy tia AM là tia phân giác của góc BAC và
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 1: Tổng các góc của một tam giác
Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
Bài 3: Hai tam giác bằng nhau
Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

