Giải SBT Toán 8 Bài tập cuối chương 7
CÂU HỎI TRẮC NGHIỆM
A. ABCD=56;
B. ABCD=65;
C. ABCD=43;
D. ABCD=34.
Lời giải:
Đáp án đúng là: B
Tỉ số của hai đường thẳng AB và CD là:
ABCD=1210=65.
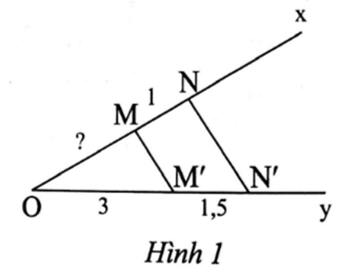
A. 3 cm;
B. 1,5 cm;
C. 2 cm;
D. 2,5 cm.
Lời giải:
Đáp án đúng là: C
Xét ∆ONN' có MM' // NN' nên theo định lí Thalès, ta có OMMN=OM'.
Suy ra OM = = 2 (cm).
Vậy OM = 2 cm.
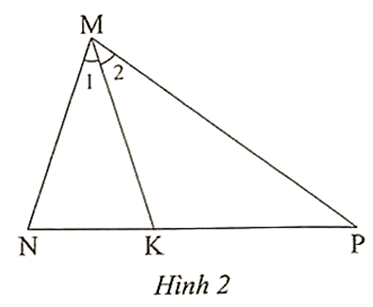
Bài 3 trang 49 sách bài tập Toán 8 Tập 2: Trong Hình 2 có . Đẳng thức nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: D
Vì MK là phân giác của trong ∆MNP nên .
Do đó (theo tính chất tỉ lệ thức).
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: A
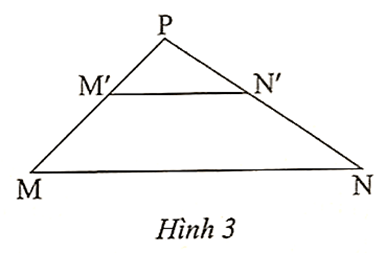
Xét ∆PMN có M'N' // MN nên theo định lí Thalès, ta có :
; ; .
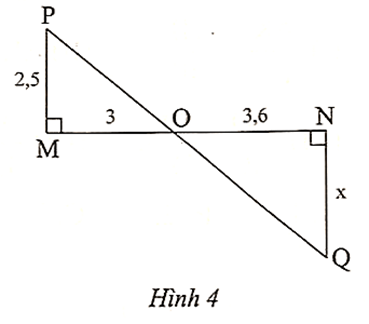
Bài 5 trang 49 sách bài tập Toán 8 Tập 2: Độ dài x trong Hình 4 là
A. 2,5;
B. 2,9;
C. 3;
D. 3,2.
Lời giải:
Đáp án đúng là: C
Vì MP ⊥ MN, NQ ⊥ MN nên MP // NQ.
Xét ∆OMP có MP // NQ, theo hệ quả của định lí Thalès, ta có .
Do đó NQ = = 3.
Vậy x = 3.
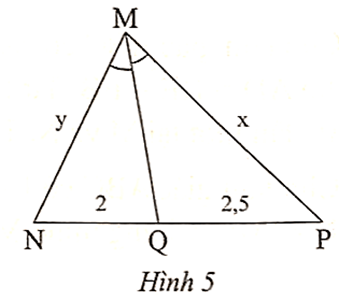
Bài 6 trang 49 sách bài tập Toán 8 Tập 2: Trong Hình 5 có MQ là tia phân giác của . Tỉ số là
A. ;
B. ;
C. ;
D. .
Lời giải:
Đáp án đúng là: B
Vì MQ là tia phân giác của trong ∆MNP nên
.
Vậy .
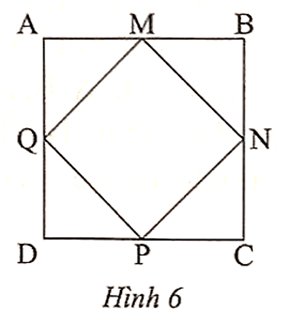
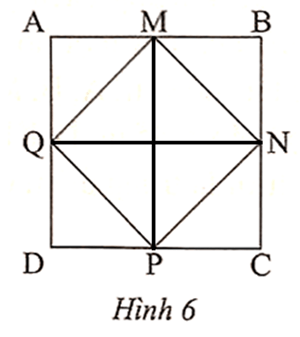
A. SMNPQ = SABCD ;
B. SMNPQ = SABCD ;
C. SMNPQ = SABCD ;
D. SMNPQ = SABCD .
Lời giải:
Đáp án đúng là: D
Vì ABCD là hình vuông và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên
AM = MB = BN = NC = CP = PD = DQ = QA.
Suy ra AM2 + QA2 = MB2 + BN2 = NC2 + CP2 = PD2 + DQ2,
Khi đó MQ2 = MN2 = NP2 = PQ2 hay MQ = MN = NP = PQ,
Do đó tứ giác MNPQ là hình thoi (1)
• Vì AM = AQ nên ∆AMQ vuông cân tại A, suy ra = 45°.
• Vì BM = BN nên ∆BMN vuông cân tại B, suy ra = 45°.
Mà + + = 180°, suy ra = 90° (2)
Từ (1) và (2) suy ra MNPQ là hình vuông.
SABCD = AB2 ; SMNPQ = MQ2
MQ2 = AM2 + QA2 =
= AB2 + AD2 = AB2 + AB2 = AB2.
Do đó SMNPQ = SABCD.
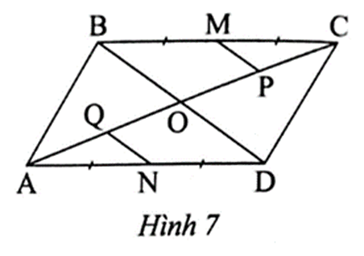
A. AQ = QP = PC ;
B. O là trung điểm PQ ;
C. MNPQ là hình bình hành ;
D. MNPQ là hình chữ nhật.
Lời giải:
Đáp án đúng là: B
• Xét ∆OAD có NA = ND và NQ // OD nên QO = QA = OA.
• Xét ∆OBD có MB = MC và MP // OB nên PO = PC = OC.
Mà ABCD là hình bình hành, suy ra OC = OA.
Do đó OQ = OP. Suy ra O là trung điểm PQ.
A. dm ;
B. 3 dm ;
C. 3,5 dm ;
D. 4 dm .
Lời giải:
Đáp án đúng là: A
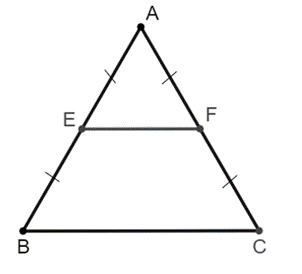
Vì EB = AB; FC = AC, AB = AC nên EB = FC = (dm)
Xét ∆ABC có EA = EB và FA = FC nên FF là đường trung bình của ∆ABC.
Suy ra EF = BC = (dm).
Chu vi hình thang EFCB bằng:
EF + FC + BC + EB = (dm)
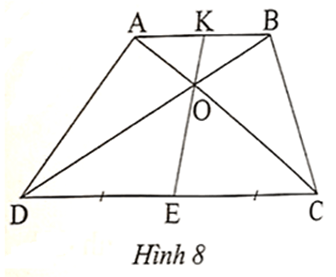
(I) ;
(II) AK = KB ;
(III) ;
(IV) .
A. 1;
B. 2;
C. 3;
D. 4.
Lời giải:
Đáp án đúng là: C
Theo hệ quả của định lí Thalès:
• Xét ∆OEC có AK // EC nên .
• Xét ∆OED có BK // DE nên .
Suy ra .
Mà EC = DE , suy ra AK = BK.
Xét ∆OCD có AB // CD, theo hệ quả của định lí Thalès, ta có:
.
Vậy có 3 khẳng định đúng là các khẳng định (I), (II), (III).
BÀI TẬP TỰ LUẬN
Lời giải:
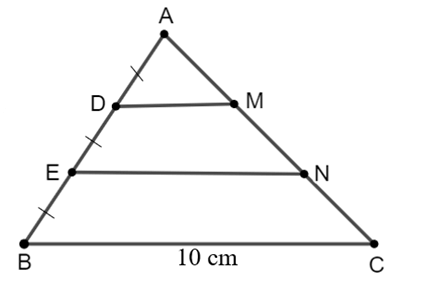
• Xét ∆ABC có DM // BC, theo hệ quả của định lí Thalès, ta có:
.
Suy ra DM = BC = .10 = (cm).
• Xét ∆ABC có EN // BC, theo hệ quả của định lí Thalès, ta có:
.
Suy ra EN = BC = .10 = (cm).
Vậy DM = cm và EN = cm.
Lời giải:
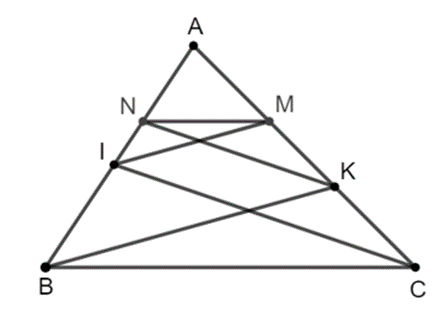
• Xét ∆ABK c
ó IM // BK, theo định lí Thalès, ta có .
• Xét ∆AIC có KN // CI, theo định lí Thalès, ta có .
Do đó , suy ra .
Xét ∆ABC có , theo định lí Thalès đảo ta có MN // BC.
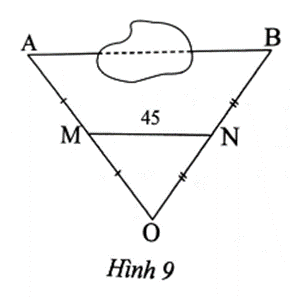
Lời giải:
Xét ∆OAB, ta có MA = MO và NB = NO.
Suy ra MN là đường trung bình của ∆ABC nên MN = AB.
Do đó AB = 2MN = 2.45 = 90 (m).
Vậy khoảng cách AB là 90 m.
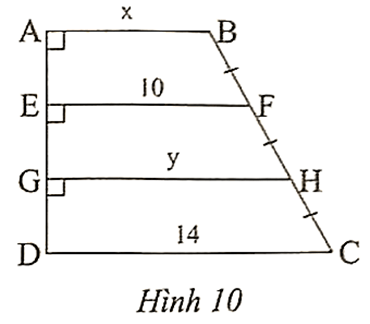
Bài 14 trang 51 sách bài tập Toán 8 Tập 2: Cho Hình 10, tính độ dài x, y.
Lời giải:
Ta có AB ⊥ AD, EF ⊥ AD, GH ⊥ AD, DG ⊥ AD.
Suy ra AB // EF // GH // DG.
• Xét tứ giác EFCD có EF // CD nên tứ giác EFCD là hình thang.
• Xét hình thang EFCD có FH= HC và GH // EF nên EG = GD.
Do đó GH là đường trung bình của hình thang EFCD.
Suy ra GH = = 12.
Tương tự, có EF là đường trung bình của hình thang ABHG.
Suy ra EF = , suy ra AB = 2EF – GH = 2.10 – 12 = 8.
Vậy x = 8 và y = 12.
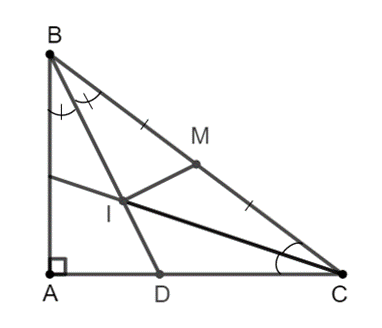
a) Tính độ dài DA, DC;
b) Tia phân giác của cắt BD ở I. Gọi M là trung điểm BC. Chứng minh = 90°.
Lời giải:
a) Xét ∆ABC vuông tại A, áp dụng định lý Pythagore, ta có:
BC2 = AB2 + AC2 = 62 + 82 =100 , suy ra BC = 10 (cm).
Vì BD là đường phân giác của trong ∆ABC nên
,
Suy ra = 1.
Do đó DA = 3.1 = 3 (cm) và DC = 5.1 = 5 (cm).
Vậy DA = 3 cm và DC = 5 cm.
b) Xét ∆ABD vuông tại A, áp dụng định lý Pythagore, ta có:
BD2 = AB2 + AD2 = 62 + 32 = 45 , suy ra BD = (cm).
Ta có CI là đường phân giác của trong ∆CBD nên
hay .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Suy ra ID = (cm) và IB = 2 (cm).
Ta có: MB = MC = BC = 5 (cm)
Xét ∆IDC và ∆IMC có
IC chung
DC = MC
Do đó ∆IDC = ∆IMC (c.g.c).
Suy ra ID = IM = (cm)
Ta có IM2 + IB2 = = 25 và MB2 = 52 = 25.
Do đó IM2 + IB2 = MB2.
Áp dụng định lý Pythagore đảo trong ∆IBM, suy ra ∆IBM vuông tại I.
Suy ra = 90°.
Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: