Giải SBT Toán 8 (Chân trời sáng tạo) Bài 3: Tính chất đường phân giác của tam giác

Giải SBT Toán 8 Bài 3: Tính chất đường phân giác của tam giác

Bài 1 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A. Tia phân giác của $\widehat{BAC}$ cắt BC tại D. Cho biết DB = 15cm, DC = 20 cm Tính độ dài AB, AC.

Lời giải:

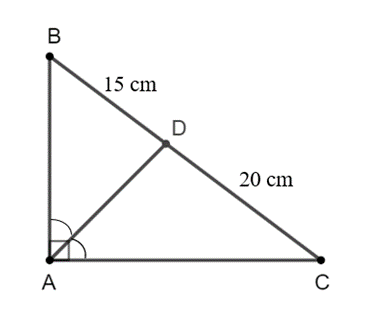
Ta có AD là phân giác của $\widehat{BAC}$ trong ∆ABC, suy ra $\frac{DB}{DC}=\frac{AB}{AC}$.

Suy ra $\frac{15}{20}=\frac{AB}{AC}$ hay $\frac{AB}{15}=\frac{AC}{20}$.

Suy ra $\frac{A{B}^2}{225}=\frac{A{C}^2}{400}=\frac{A{B}^2+A{C}^2}{225+400}=\frac{B{C}^2}{625}$ (áp dụng định lí Pythagore trong ∆ABC vuông).

Ta có BC = BD + DC = 15 + 20 = 35 (cm).

Nên $\frac{A{B}^2}{225}=\frac{A{C}^2}{400}=\frac{{35}^2}{625}=\frac{49}{25}$.

Suy ra  AB² = $\frac{49.225}{25}$ =  441 và AC² = $\frac{49.400}{25}$ = 784.

Vậy AB = 21 cm; AC = 28 cm.

Bài 2 trang 48 sách bài tập Toán 8 Tập 2: Cho ∆ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm. Tia phân giác của $\widehat{BAC}$ cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A cắt BC tại E. Tính độ dài DB, DC, EB.

Lời giải:

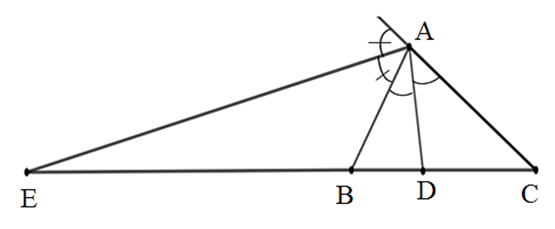
• Vì AD là phân giác của $\widehat{BAC}$ trong ∆ABC nên ta có

$\frac{DB}{DC}=\frac{AB}{AC}=\frac{6}{9}=\frac{2}{3}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{DB}{2}=\frac{DC}{3}=\frac{DB+DC}{2+3}=\frac{BC}{5}=\frac{10}{5}$ = 2.

Suy ra $\frac{DB}{2}$ = 2 và $\frac{DC}{3}$ = 2.

Do đó DB = 4 cm; DC = 6 cm.

• Vì AE là phân giác ngoài tại đỉnh A của ∆ABC nên ta có

$\frac{EB}{EC}=\frac{AB}{AC}=\frac{6}{9}=\frac{2}{3}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{EC}{3}=\frac{EB}{2}=\frac{EC-EB}{3-2}=\frac{BC}{1}$ = 10.

Do đó $\frac{EB}{2}$ = 10 suy ra EB = 20 cm.

Vậy DB = 4 cm, DC = 6 cm, EB = 20 cm.

Bài 3 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có các đường phân giác AD, BE, CF (D ∈ BC, E ∈ AC, F ∈ AB) cắt nhau tại I. Chứng minh:

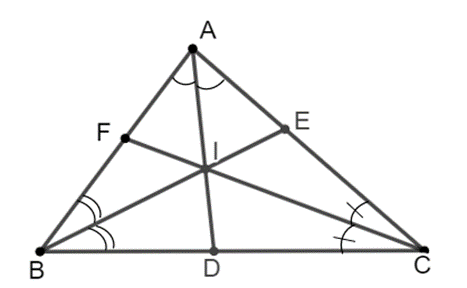
a) $\frac{DI}{DA}=\frac{BC}{AB+BC+CA}$;

b) $\frac{DI}{DA}+\frac{EI}{EB}+\frac{FI}{FC}$ = 1.

Lời giải:

a) • Vì BI là phân giác của $\widehat{ABC}$ trong ∆ABC nên ta có $\frac{IA}{ID}=\frac{AB}{BD}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{IA}{AB}=\frac{ID}{BD}=\frac{IA+ID}{AB+BD}=\frac{AD}{AB+BD}$ suy ra $\frac{ID}{AD}=\frac{BD}{AB+BD}$        (1)

• Vì CI là phân giác của $\widehat{ACB}$ trong ∆ABC nên ta có $\frac{IA}{ID}=\frac{CA}{CD}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{IA}{CA}=\frac{DI}{CD}=\frac{IA+ID}{CA+CD}=\frac{DA}{CA+CD}$ suy ra $\frac{DI}{AD}=\frac{CD}{CA+CD}$        (2)

Từ (1) và (2) suy ra: $\frac{BD}{AB+BD}=\frac{CD}{CA+CD}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{BD}{AB+BD}=\frac{CD}{CA+CD}$$=\frac{BD+CD}{AB+BD+CA+CD}$$=\frac{BC}{AB+BC+CA}$    (3)

Từ (1), (2) và (3) suy ra: $\frac{DI}{DA}=\frac{BC}{AB+BC+CA}$.

b) Tượng tự câu a) ta có: $\frac{EI}{EB}=\frac{CA}{AB+BC+CA}$và $\frac{FI}{FC}=\frac{AB}{AB+BC+CA}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{DI}{DA}+\frac{EI}{EB}+\frac{FI}{FC}$ = $\frac{BC}{AB+BC+CA}$ + $\frac{CA}{AB+BC+CA}$ + $\frac{AB}{AB+BC+CA}$

= $\frac{AB+BC+CA}{AB+BC+CA}$ = 1.

Bài 4 trang 48 sách bài tập Toán 8 Tập 2: Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN // AD.

Lời giải:

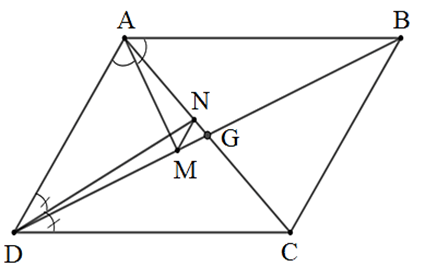
Gọi G là giao điểm của AC và BD.

• Vì DN là phân giác của $\widehat{ADC}$ trong ∆ADC nên $\frac{NA}{NC}=\frac{AD}{DC}$.

• Vì AM là phân giác của $\widehat{BAD}$ trong ∆ABD nên $\frac{MD}{MB}=\frac{AD}{AB}$ = $\frac{AD}{DC}$ (vì AB = DC).

Suy ra $\frac{MD}{MB}=\frac{NA}{NC}$.

Do đó $\frac{NA}{MD}=\frac{NC}{MB}=\frac{NA+NC}{MD+MB}=\frac{AC}{BD}=\frac{AG}{DG}$ (AC = 2AG; BD = 2BG)

Khi đó $\frac{NA}{AG}=\frac{MD}{DG}$.

Xét ∆AGD có $\frac{NA}{AG}=\frac{MD}{DG}$ nên theo định lí Thalès đảo, ta có MN // AD.

Bài 5 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC cân ở A. Tia phân giác của $\widehat{ABC}$ cắt AC tại D. Cho biết BC= 10 cm, AB = 15 cm. Tính DA, DC.

Lời giải:

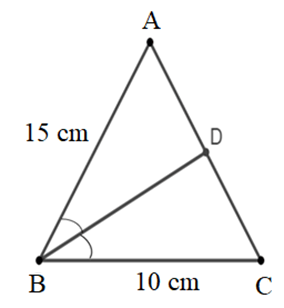
Vì BD là phân giác của $\widehat{ABC}$ trong ∆ABC nên $\frac{DA}{DC}=\frac{BA}{BC}=\frac{15}{10}=\frac{3}{2}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{DA}{3}=\frac{DC}{2}=\frac{DA+DC}{3+2}=\frac{AC}{5}$.

Mà ∆ABC cân ở A nên AC = AB = 15 cm.

Suy ra $\frac{DA}{3}=\frac{DC}{2}=\frac{15}{5}$ = 3.

Do đó DA = 3.3 = 9 (cm) và DC = 3.2 = 6 (cm).

Vậy DA = 9 cm, DC = 6 cm.

Bài 6 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có đường trung tuyến AM (M ∈ BC). Tia phân giác của $\widehat{AMB}$ cắt AB tại D, tia phân giác của $\widehat{AMC}$ cắt AC tại E.

a) Chứng minh DE // BC;

b) Gọi I là giao điểm của DE với AM. Chứng mình I là trung điểm của DE.

Lời giải:

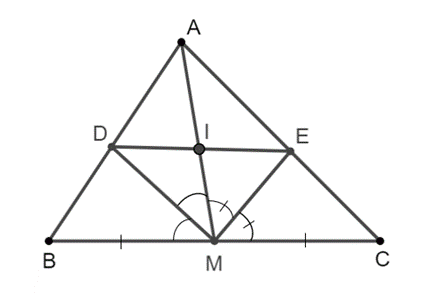
a) Vì MD là phân giác của $\widehat{AMB}$ trong ∆ABM nên $\frac{DA}{DB}=\frac{MA}{MB}$.

Vì ME là phân giác của $\widehat{AMC}$ trong ∆ABC nên $\frac{EA}{EC}=\frac{MA}{MC}$.

Mà MB = MC, suy ra $\frac{DA}{DB}=\frac{EA}{EC}$.

Xét ∆ABC có $\frac{DA}{DB}=\frac{EA}{EC}$ nên theo định lí Thalès đảo, ta có DE // BC.

b) Theo hệ quả của định lí Thalès:

• Xét ∆ABM có DI // MB (vì I ∈ DE, M ∈ BC), ta có $\frac{AI}{AM}=\frac{DI}{MB}$.

• Xét ∆ACM có EI // MC, ta có $\frac{AI}{AM}=\frac{IE}{MC}$.

Suy ra $\frac{IE}{MC}=\frac{DI}{MB}$, mà MC = MB, suy ra IE = DI.

Vậy I là trung điểm của DE.

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: