Giải SBT Toán 8 (Chân trời sáng tạo) Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Giải SBT Toán 8 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

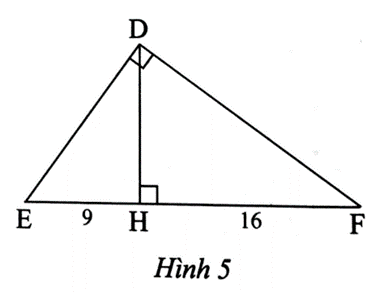
Bài 1 trang 68 SBT Toán 8 Tập 2: Quan sát Hình 5.

a) Chứng minh rằng ∆HDE ᔕ ∆HFD.

b) Tính độ dài HD.

Lời giải:

a) Xét ∆HDE vuông tại H và ∆HFD vuông tại H có

$\widehat{HDE}=\widehat{HFD}$ (cùng phụ với $\widehat{HDF}$).

Do đó ∆HDE ᔕ ∆HFD (g.g).

b) Ta có ∆HDE ᔕ ∆HFD, suy ra $\frac{HD}{HF}=\frac{HE}{HD}$.

Do đó HD² = HE.HF = 9.16 = 144, suy ra HD = 12.

Vậy HD = 12.

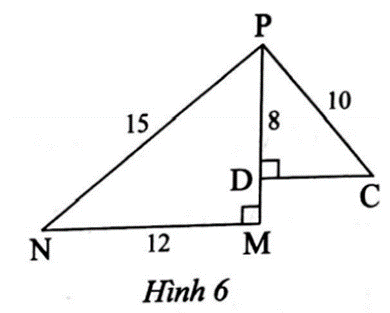
Bài 2 trang 68 SBT Toán 8 Tập 2: Quan sát Hình 6, chứng minh rằng:

a) ∆MNP ᔕ ∆DPC.

b) NP ⊥ PC.

Lời giải:

a) Ta có $\frac{MN}{DP}=\frac{12}{8}=\frac{3}{2}$ và $\frac{PN}{CP}=\frac{15}{10}=\frac{3}{2}$.

Xét ∆MNP vuông tại M và ∆DPC vuông tại D có $\frac{MN}{DP}=\frac{PN}{CP}$.

Do đó ∆MNP ᔕ ∆DPC.

b) Ta có ∆MNP ᔕ ∆DPC, suy ra $\widehat{MNP}=\widehat{DPC}$.

Mà $\widehat{MNP}+\widehat{MPN}=90°$ (∆MNP vuông tại M).

Do đó $\widehat{DPC}+\widehat{MPN}=90°$, suy ra NP ⊥ PC.

Bài 3 trang 68 SBT Toán 8 Tập 2: Quan sát Hình 7, biết tứ giác ABHD là hình chữ nhật. Chứng minh rằng:

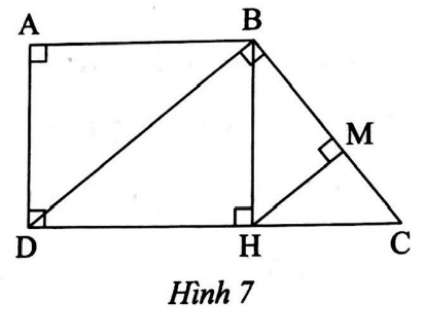
a) BD² = BD . DC.

b) AD² = BM . BC.

Lời giải:

a) Xét ∆ABD vuông tại A và ∆BDC vuông tại B có $\widehat{ABC}=\widehat{BDC}$ (so le trong).

Do đó ∆ABD ᔕ ∆BDC (g.g).

Suy ra $\frac{AB}{BD}=\frac{BD}{DC}$. Do đó BD² = BD . DC.

b) Ta có ∆BMH vuông tại M và ∆BHC vuông tại H có $\widehat{B}$ chung.

Do đó ∆BMH ᔕ ∆BHC (g.g).

Suy ra $\frac{BM}{BH}=\frac{BH}{BC}$. Do đó BH² = BM . BC.

Tứ giác ABHD là hình chữ nhật, suy ra AD = BH.

Vậy AD² = BM . BC.

Bài 4 trang 68 SBT Toán 8 Tập 2: Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC ⊥ BD, chứng minh rằng:

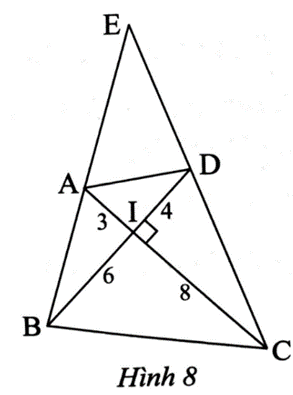
a) ∆AIB ᔕ ∆DIC.

b) EA . EB = EC . ED.

Lời giải:

a) Ta có $\frac{IA}{ID}=\frac{3}{4}$; $\frac{IB}{IC}=\frac{6}{8}=\frac{3}{4}$ suy ra $\frac{IA}{ID}=\frac{IB}{IC}$.

Xét ∆AIB vuông tại I và ∆DIC vuông tại I có $\frac{IA}{ID}=\frac{IB}{IC}$.

Suy ra ∆AIB ᔕ ∆DIC

b) Ta có ∆AIB ᔕ ∆DIC, suy ra $\widehat{ABI}=\widehat{DCI}$.

Xét ∆EDB và ∆EAC có

$\widehat{E}$ chung và $\widehat{ABI}=\widehat{DCI}$.

Do đó ∆EDB ᔕ ∆EAC (g.g).

Suy ra $\frac{ED}{EA}=\frac{EB}{EC}$. Do đó EA . EB = EC . ED (đpcm).

Bài 5 trang 69 SBT Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP theo tỉ số đồng dạng $k=\frac{AB}{MN}=\frac{2}{3}$. Kẻ đường cao AH của tam giác ABC và đường cao MK của tam giác MNP.

a) Chứng minh rằng ∆ABH ᔕ ∆MNK. Tính tỉ số $\frac{AH}{MK}=\frac{2}{3}$.

b) Biết diện tích tam giác ABC bằng 56 cm². Tính diện tích tam giác MNP.

Lời giải:

a) Ta có ∆ABC ᔕ ∆MNP, suy ra $\widehat{B}=\widehat{N}$

Xét ∆ABH vuông tại H và ∆MNK vuông tại K có $\widehat{B}=\widehat{N}$.

Do đó ∆ABH ᔕ ∆MNK (g.g).

Suy ra $\frac{AH}{MK}=\frac{AB}{MN}=\frac{2}{3}$.

Vậy $\frac{AH}{MK}=\frac{2}{3}$.

b) Ta có ∆ABC ᔕ ∆MNP, suy ra $\frac{S_{\Delta ABC}}{S_{\Delta MNP}}={\left(\frac{2}{3}\right)}^2$ hay $\frac{56}{S_{\Delta MNP}}=\frac{4}{9}$.

Do đó $S_{\Delta MNP}=\frac{56.9}{4}=126$ (cm²).

Vậy diện tích tam giác MNP là 126 cm².

Bài 6 trang 69 SBT Toán 8 Tập 2: Người ta dùng một gương phẳng đề đo chiều cao của một căn nhà (Hình 9). Đặt tấm gương nằm trên mặt phẳng nằm ngang (điểm C), mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát lùi dần cho đến khi nhìn thấy ảnh của đỉnh căn nhà trong gương. Cho biết $\widehat{ACB}=\widehat{MCN}$, AB = 1,65 m, BC = 4 m, NC = 20 m. Tính chiều cao MN của căn nhà.

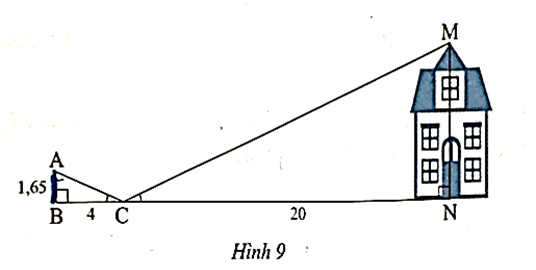
Lời giải:

Xét ∆ABC vuông tại B và ∆MNC vuông tại N có $\widehat{ACB}=\widehat{MCN}$.

Do đó ∆ABC ᔕ ∆MNC (g.g).

Suy ra $\frac{AB}{MN}=\frac{BC}{NC}$ hay $\frac{1,65}{MN}=\frac{4}{20}$.

Do đó $MN=\frac{1,65.20}{4}=8,25$ (m).

Vậy chiều cao MN của căn nhà là 8,25 m.

Bài 7 trang 69 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A. Tia phân giác của $\widehat{A}$ cắt cạnh huyền BC tại M. Qua M kẻ đường thẳng vuông góc với BC và cắt AC tại N. Chứng minh rằng:

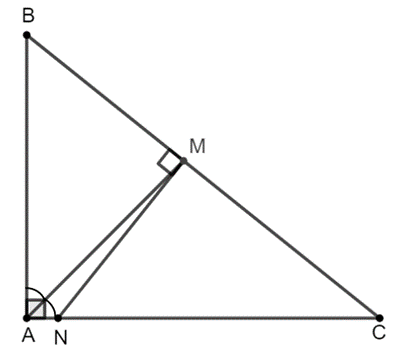
a) ∆MNC ᔕ ∆ABC.

b) MN = MB.

Lời giải:

a) Xét ∆MNC vuông tại M và ∆ABC vuông tại A có $\widehat{C}$ chung.

Do đó ∆MNC ᔕ ∆ABC (g.g).

b) Ta có ∆MNC ᔕ ∆ABC, suy ra $\frac{MN}{AB}=\frac{MC}{AC}$ (1)

Xét ∆ABC có AM là phân giác của $\widehat{A}$ có

$\frac{MB}{MC}=\frac{AB}{AC}$, suy ra $\frac{MB}{AB}=\frac{MC}{AC}$ (2)

Từ (1) và (2), suy ra $\frac{MB}{AB}=\frac{MN}{AB}$.

Do đó MN = MB (đpcm).

Bài 8 trang 69 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB < AC) và kẻ đường cao AH. Tia phân giác của $\widehat{B}$ cắt AC tại E và cắt AH tại F. Chứng minh rằng:

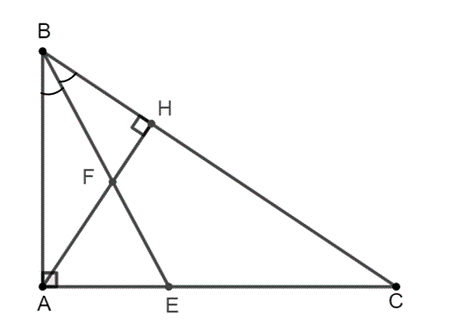
a) AB . HF = AE . HB.

b) AE = AF.

c) AE² = EC . FH.

Lời giải:

a) Vì BE là tia phân giác của $\widehat{ABC}$ nên $\widehat{ABE}=\widehat{CBE}$.

Xét ∆ABE vuông tại A và ∆HBF vuông tại H có

$\widehat{ABE}=\widehat{HBF}$ ($\widehat{ABE}=\widehat{CBE}$)

Do đó ∆ABE ᔕ ∆HBF (g.g)

Suy ra $\frac{AB}{HB}=\frac{AE}{HF}$. Do đó AB . HF = AE . HB (đpcm).

b) Ta có ∆ABE ᔕ ∆HBF.

Suy ra $\widehat{AEB}=\widehat{HFB}$ hay $\widehat{AEF}=\widehat{HFB}$ (các góc tương ứng).

Mà $\widehat{AFE}=\widehat{HFB}$ (đối đỉnh) nên $\widehat{AEF}=\widehat{AFE}$. Suy ra ∆AEF cân tại A.

Do đó AE = AF.

c) Xét ∆ABC có BE là tia phân giác của $\widehat{B}$, suy ra $\frac{AB}{BC}=\frac{AE}{EC}$ (1)

Xét ∆ABH có BF là tia phân giác của $\widehat{B}$, suy ra $\frac{FH}{AF}=\frac{BH}{AB}$ (2)

Xét ∆ABH vuông tại H và ∆ABC vuông tại A có $\widehat{B}$ chung.

Do đó ∆ABH ᔕ ∆CBA, suy ra $\frac{AB}{BC}=\frac{BH}{AB}$ (3)

Từ (1); (2) và (3) suy ra $\frac{AE}{EC}=\frac{FH}{AF}$.

Do đó AE . AF = EC . FH.

Mà AE = AF, suy ra AE² = EC . FH (đpcm).

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: