Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Tia phân giác của góc ABC cắt AC tại D

Bài 15 trang 51 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Tia phân giác của $\widehat{ABC}$ cắt AC tại D.

a) Tính độ dài DA, DC;

b) Tia phân giác của $\widehat{ACB}$ cắt BD ở I. Gọi M là trung điểm BC. Chứng minh $\widehat{BIM}$ = 90°.

Trả lời

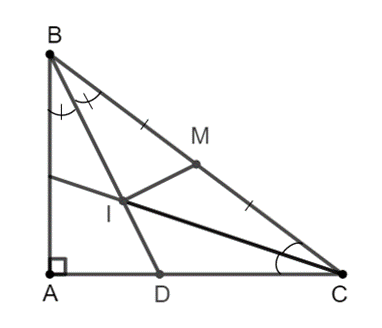
a) Xét ∆ABC vuông tại A, áp dụng định lý Pythagore, ta có:

BC² = AB² + AC² = 6² + 8² =100 , suy ra BC =  10 (cm).

Vì BD là đường phân giác của $\widehat{ABC}$ trong ∆ABC nên

$\frac{DA}{DC}=\frac{BA}{BC}=\frac{6}{10}=\frac{3}{5}$,

Suy ra $\frac{DA}{3}=\frac{DC}{5}=\frac{DA+DC}{3+5}=\frac{AC}{8}=\frac{8}{8}$ = 1.

Do đó DA = 3.1 = 3 (cm) và DC = 5.1 = 5 (cm).

Vậy DA = 3 cm và DC = 5 cm.

b) Xét ∆ABD vuông tại A, áp dụng định lý Pythagore, ta có:

BD² = AB² + AD² = 6² + 3² = 45 , suy ra BD = $3\sqrt{5}$ (cm).

Ta có CI là đường phân giác của $\widehat{DCB}$ trong ∆CBD nên

$\frac{ID}{IB}=\frac{CD}{CB}=\frac{5}{10}=\frac{1}{2}$ hay $\frac{ID}{1}=\frac{IB}{2}$.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{ID}{1}=\frac{IB}{2}=\frac{ID+IB}{1+2}=\frac{BD}{3}=\frac{3\sqrt{5}}{3}=\sqrt{5}$.

Suy ra ID = $\sqrt{5}$ (cm) và IB = 2$\sqrt{5}$ (cm).

Ta có: MB = MC = $\frac{1}{2}$BC = 5 (cm)

Xét ∆IDC và ∆IMC có

IC chung

$\widehat{DCI}=\widehat{MCI}$

DC = MC

Do đó ∆IDC = ∆IMC (c.g.c).

Suy ra ID = IM = $\sqrt{5}$ (cm)

Ta có  IM² + IB² = ${\left(\sqrt{5}\right)}^2+{\left(2\sqrt{5}\right)}^2$ = 25 và MB² = 5² = 25.

Do đó IM² + IB² = MB².

Áp dụng định lý Pythagore đảo trong ∆IBM, suy ra ∆IBM vuông tại I.

Suy ra $\widehat{BIM}$ = 90°.

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông