Cho hình thang ABCD (AB // CD) và DE = EC (Hình 8). Gọi O là giao điểm của AC và BD, K là giao điểm của EO và AB

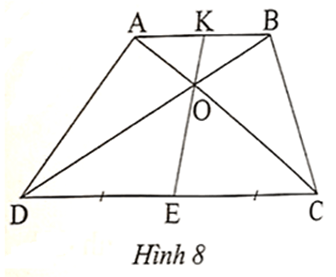
Bài 10 trang 49 sách bài tập Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) và DE = EC (Hình 8). Gọi O là giao điểm của AC và BD, K là giao điểm của EO và AB. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?

(I) $\frac{AK}{EC}=\frac{KB}{DE}$;

(II) AK = KB ;

(III) $\frac{AO}{AC}=\frac{AB}{DC}$;

(IV) $\frac{AK}{EC}=\frac{OB}{OD}$.

A. 1;

B. 2;

C. 3;

D. 4.

Trả lời

Đáp án đúng là: C

Theo hệ quả của định lí Thalès:

• Xét ∆OEC có AK // EC nên $\frac{AK}{EC}=\frac{BK}{DE}$.

• Xét ∆OED có BK // DE nên $\frac{BK}{DE}=\frac{OK}{KE}$.

Suy ra $\frac{AK}{EC}=\frac{BK}{DE}$.

Mà EC = DE , suy ra AK = BK.

Xét ∆OCD có AB // CD, theo hệ quả của định lí Thalès, ta có:

$\frac{AO}{AC}=\frac{AB}{DC}=\frac{OB}{OD}$.

Vậy có 3 khẳng định đúng là các khẳng định (I), (II), (III).

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông