Giải SBT Toán 8 (Chân trời sáng tạo) Bài 2: Các trường hợp đồng dạng của hai tam giác

Giải SBT Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác

Trường hợp đồng dạng thứ nhất (c.c.c)

Bài 1 trang 62 SBT Toán 8 Tập 2: Tam giác ABC có độ dài AB = 9 cm, AC = 12 cm, BC = 14 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 61.25 cm. Hãy tính độ dài các cạnh của tam giác A'B'C'.

Lời giải:

Ta có ∆A’B’C’ ᔕ ∆ABC, suy ra

$\frac{A\text{'}B\text{'}}{AB}=\frac{A\text{'}C\text{'}}{AC}=\frac{B\text{'}C\text{'}}{BC}$ hay $\frac{A\text{'}B\text{'}}{9}=\frac{A\text{'}C\text{'}}{12}=\frac{B\text{'}C\text{'}}{14}$

Áp dụng tính chất tỉ lệ thức, có:

$\frac{A\text{'}B\text{'}}{9}=\frac{A\text{'}C\text{'}}{12}=\frac{B\text{'}C\text{'}}{14}$ = $\frac{A\text{'}B\text{'}+A\text{'}C\text{'}+B\text{'}C\text{'}}{9+12+14}=\frac{61,25}{35}=\frac{7}{4}$.

Suy ra $\frac{A\text{'}B\text{'}}{9}=\frac{7}{4}$; $\frac{A\text{'}C\text{'}}{12}=\frac{7}{4}$ và $\frac{B\text{'}C\text{'}}{14}=\frac{7}{4}$.

Do đó $A\text{'}B\text{'}=\frac{7.9}{4}=15,75$; $A\text{'}C\text{'}=\frac{7.12}{4}=21$ và $B\text{'}C\text{'}=\frac{7.14}{4}=24,5$.

Vậy A’B’ = 15,75 cm ; A’C’ = 21 cm và B’C’ = 24,5 cm.

Bài 2 trang 62 SBT Toán 8 Tập 2: a) Tam giác ABC và MBN (Hình 4) có đồng dạng với nhau không? Vì sao?

b) Biết tam giác ABC có chu vi bằng 15 cm. Tính chu vi tam giác MBN.

Lời giải:

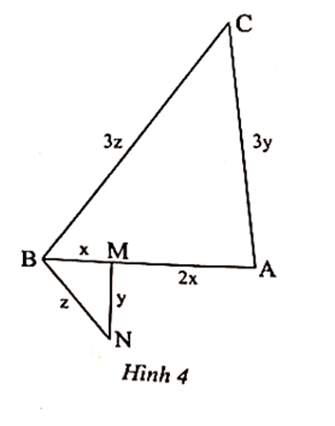
a) Ta có AB = AM + MB = x + 2x = 3x.

Ta lại có $\frac{MB}{AB}=\frac{x}{3x}=\frac{1}{3}$; $\frac{MN}{AC}=\frac{y}{3y}=\frac{1}{3}$ và $\frac{NB}{BC}=\frac{z}{3z}=\frac{1}{3}$.

Xét ∆MBN và ∆ABC có: $\frac{MB}{AB}=\frac{MN}{AC}=\frac{NB}{BC}$.

Suy ra ∆MBN ᔕ ∆ABC (c.c.c).

b) Ta có MBN ᔕ ∆ABC.

Khi đó, tỉ số chu vi của hai tam giác bằng tỉ số đồng dạng là:

$\frac{P_{MBN}}{P_{ABC}}=\frac{1}{3}$ hay $\frac{P_{MBN}}{15}=\frac{1}{3}$.

Do đó $P_{MBN}=\frac{1.15}{3}=5$.

Vậy chu vi tam giác MBN là 5 cm.

Bài 3 trang 63 SBT Toán 8 Tập 2: Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm, AB = 8 cm, NA = 12 cm, NB = 6,4 cm. Chứng minh rằng:

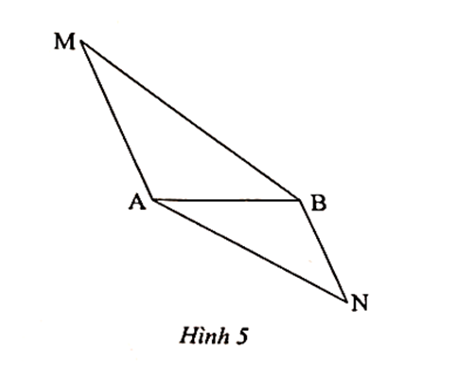
a) ∆MAB ᔕ ∆ABN.

b) Tứ giác AMBN là hình thang.

Lời giải:

a) Ta có $\frac{MA}{AB}=\frac{10}{8}=\frac{5}{4}$; $\frac{AB}{BN}=\frac{8}{6,4}=\frac{5}{4}$; $\frac{MB}{AN}=\frac{15}{12}=\frac{5}{4}$.

Xét ∆MAB và ∆ABN có $\frac{MA}{AB}=\frac{AB}{BN}=\frac{MB}{AN}$.

Do đó ∆MAB ᔕ ∆ABN (c.c.c).

b) Ta có ∆MAB ᔕ ∆ABN, suy ra $\widehat{MAB}=\widehat{NBA}$.

Mà $\widehat{MAB}$ và $\widehat{NBA}$ là hai góc so le trong, suy ra MA // BN.

Suy ra tứ giác AMBN là hình thang.

Bài 4 trang 63 SBT Toán 8 Tập 2: Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng với nhau (Hình 6). Bồn hoa thứ nhất có chu vi 7,5 m và cạnh dài nhất là 3,5 m. Bồn hoa thứ hai có chu vi 4,5 m. Tính độ dài cạnh dài nhất của bồn hoa thứ hai.

Lời giải:

Ta có ∆ABC ᔕ ∆DEF, suy ra $\frac{BC}{EF}=\frac{P_{\Delta ABC}}{P_{\Delta DEF}}=\frac{7,5}{4,5}=\frac{5}{3}$.

Suy ra $\frac{3,5}{EF}=\frac{5}{3}$, suy ra $EF=\frac{3.3,5}{5}=2,1$ (m).

Vậy độ dài cạnh dài nhất của bồn hoa thứ hai là 2,1 m.

Trường hợp đồng dạng thứ hai (c.g.c)

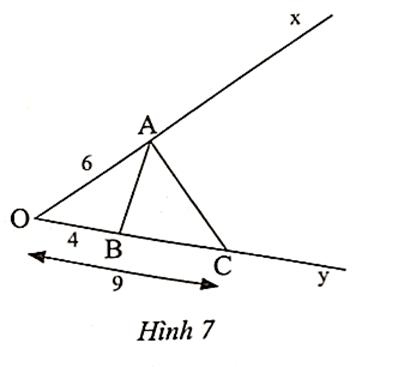
Bài 5 trang 63 SBT Toán 8 Tập 2: Quan sát Hình 7. Chứng minh rằng $\widehat{OBA}=\widehat{OAC}$.

Lời giải:

Ta có $\frac{OB}{OA}=\frac{4}{6}=\frac{2}{3}$; $\frac{OA}{OC}=\frac{6}{9}=\frac{2}{3}$, suy ra $\frac{OB}{OA}=\frac{OA}{OC}$.

Xét ∆OAB và ∆OCA có $\frac{OB}{OA}=\frac{OA}{OC}$ và $\widehat{O}$ chung.

Do đó ∆OAB ᔕ ∆OCA (c.g.c).

Suy ra $\widehat{OBA}=\widehat{OAC}$ (hai góc tương ứng).

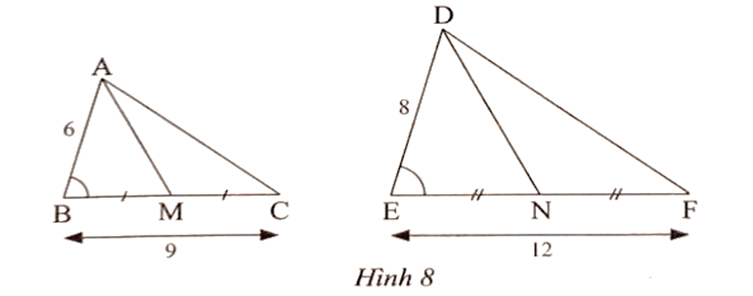
Bài 6 trang 63 SBT Toán 8 Tập 2: Quan sát Hình 8.

a) Chứng minh rằng ∆ABC ᔕ ∆DEF.

b) Cho biết AM là đường trung tuyến của tam giác ABC, DN là đường trung tuyến của tam giác DEF và AM = 5,1 cm. Tính độ dài DN.

Lời giải:

a) Ta có $\frac{AB}{DE}=\frac{6}{8}=\frac{3}{4}$; $\frac{BC}{EF}=\frac{9}{12}=\frac{3}{4}$, suy ra $\frac{AB}{DE}=\frac{BC}{EF}$.

Xét ∆ABC và ∆DEF có

$\frac{AB}{DE}=\frac{BC}{EF}$ và $\widehat{B}=\widehat{E}$

Do đó ∆ABC ᔕ ∆DEF (c.g.c).

b) Ta có ∆ABC ᔕ ∆DEF nên

$\frac{AM}{DN}=\frac{AB}{DE}=\frac{3}{4}$, suy ra $\frac{5,1}{DN}=\frac{3}{4}$.

Do đó $DN=\frac{4.5,1}{3}=6,8$.

Vậy DN = 6,8 cm.

Bài 7 trang 63 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6. Chứng minh rằng:

a) ∆ANM ᔕ ∆ABC.

b) $\widehat{ABN}=\widehat{ACM}$.

Lời giải:

a) Xét ∆ANM và ∆ABC có

$\frac{AN}{AB}=\frac{AM}{AC}=\frac{1}{2}$, $\widehat{\text{A}}$ chung.

Do đó ∆ABC ᔕ ∆DEF (c.g.c).

b) Ta có $\frac{AN}{AB}=\frac{AM}{AC}$, suy ra $\frac{AN}{AM}=\frac{AB}{AC}$.

Xét ∆ANB và ∆AMC có

$\frac{AN}{AM}=\frac{AB}{AC}$ và $\widehat{A}$ chung.

Do đó ∆ANB ᔕ ∆AMC (c.g.c).

Suy ra $\widehat{ABN}=\widehat{ACM}$ (hai góc tương ứng).

Bài 8 trang 64 SBT Toán 8 Tập 2: Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng:

a) $\frac{CA}{CF}=\frac{ME}{MF}$ và $\frac{BE}{BA}=\frac{ME}{MF}$.

b) ∆BCE ᔕ ∆CFB.

Lời giải:

a) Xét ∆MCF có AE // CM (vì AB // CM), theo định lí Thalès ta có:

$\frac{CA}{CF}=\frac{ME}{MF}$ (1)

Xét ∆BEM có AF // BM (vì AC // BM), theo hệ quả của định lí Thalès ta có:

$\frac{AE}{BE}=\frac{EF}{ME}$.

Ta có $\frac{AE}{BE}+1=\frac{EF}{ME}+1$ hay $\frac{AE}{BE}+\frac{BE}{BE}=\frac{EF}{ME}+\frac{ME}{ME}$.

Suy ra $\frac{BA}{BE}=\frac{MF}{ME}$ hay $\frac{BE}{BA}=\frac{ME}{MF}$ (2)

b) Từ (1) và (2), suy ra $\frac{CA}{CF}=\frac{BE}{BA}$, mà AB = BC = AC. Suy ra $\frac{BC}{CF}=\frac{BE}{BC}$.

Xét ∆BCE và ∆CFB có $\frac{BC}{CF}=\frac{BE}{BC}$ và $\widehat{EBC}=\widehat{BCF}$ (∆ABC đều).

Do đó ∆BCE ᔕ ∆CFB (c.g.c).

Trường hợp đồng dạng thứ ba (g.g)

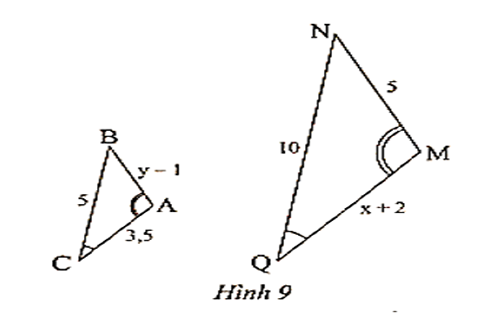
Bài 9 trang 64 SBT Toán 8 Tập 2: Quan sát Hình 9.

a) Chứng minh rằng ∆ABC ᔕ ∆MNQ.

b) Tính x, y.

Lời giải:

a) Xét ∆ABC và ∆MNQ có

$\widehat{A}=\widehat{M}$ và $\widehat{C}=\widehat{Q}$

Do đó ∆ABC ᔕ ∆MNQ (g.g)

b) Ta có ∆ABC ᔕ ∆MNQ, suy ra

$\frac{AB}{MN}=\frac{AC}{MQ}=\frac{BC}{NQ}$ hay $\frac{y-1}{5}=\frac{3,5}{x+2}=\frac{5}{10}=\frac{1}{2}$.

Suy ra $\frac{y-1}{5}=\frac{1}{2}$ và $\frac{3,5}{x+2}=\frac{1}{2}$.

Do đó $y-1=\frac{5}{2}=2,5$ và x + 2 =7.

Suy ra y = 2,5 + 1 = 3,5 và x = 7 – 2 = 5.

Vây x = 5 và y = 3,5.

Bài 10 trang 64 SBT Toán 8 Tập 2: Trong Hình 10, cho biết AB = 4,2; IA = 6; IC = 10; $\widehat{ABI}$ = 60°; $\widehat{CDx}$ = 120°. Tính độ dài CD.

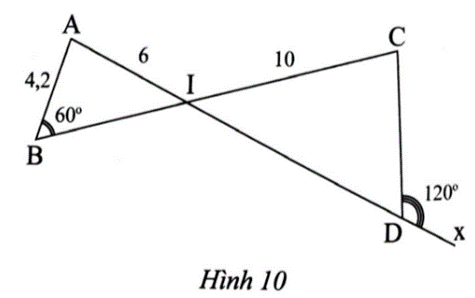
Lời giải:

Ta có $\widehat{CDx}+\widehat{CDI}=180°$ (hai góc kề bù).

Suy ra $\widehat{CDI}=180°-\widehat{CDI}$ = 180° - 120° = 60°.

Xét ∆IAB và ∆ICD có

$\widehat{ABI}=\widehat{CDI}$ (= 60°) và $\widehat{AIB}=\widehat{CID}$ (đối đỉnh).

Suy ra ∆IAB ᔕ ∆ICD (g.g).

Suy ra $\frac{IA}{IC}=\frac{AB}{CD}$ hay $\frac{6}{10}=\frac{4,2}{CD}$.

Do đó $CD=\frac{4,2.10}{6}=7$.

Vậy CD = 7.

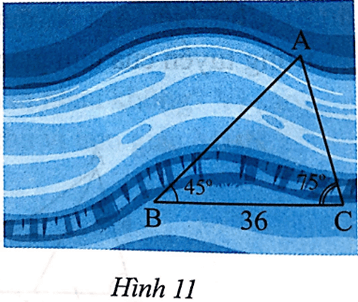
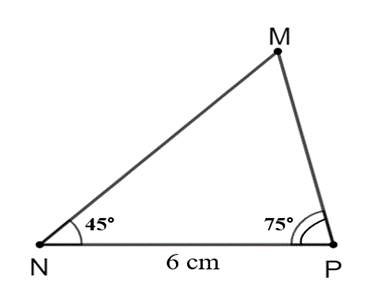
Bài 11 trang 64 SBT Toán 8 Tập 2: Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm, $\widehat{N}=45°$, $\widehat{P}=75°$.

a) Chứng minh rằng ∆MNP ᔕ ∆ABC.

b) Dùng thước đo chiều dài cạnh MP của ∆MNP. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 11.

Lời giải:

a) Xét ∆MNP và ∆ABC có

$\widehat{N}=\widehat{B}$ (= 45°) và $\widehat{P}=\widehat{C}$ (= 75°).

Do đó ∆MNP ᔕ ∆ABC (g.g).

b) Ta có MP = 4 cm.

Ta có ∆MNP ᔕ ∆ABC suy ra $\frac{MP}{AC}=\frac{NP}{BC}$ hay $\frac{4}{AC}=\frac{6}{36}$.

Do đó $AC=\frac{4.36}{6}=24$.

Vậy AC = 24 cm.

Bài 12 trang 64 SBT Toán 8 Tập 2: Trong Hình 12, cho tứ giác ABCD là hình thang. Biết DB là tia phân giác của $\widehat{ADC}$ và $\widehat{DAB}=\widehat{DBC}$. Chứng minh rằng:

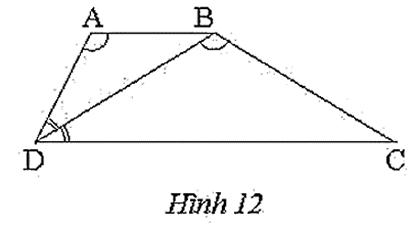
a) ∆ABD ᔕ ∆BDC.

b) BD² = AB . DC.

Lời giải:

a) Xét ∆ABD và ∆BDC có

$\widehat{DAB}=\widehat{DBC}$ và $\widehat{ADB}=\widehat{BDC}$ (DB là tia phân giác của $\widehat{ADC}$).

Do đó ∆ABD ᔕ ∆BDC (g.g).

b) Ta có ∆ABD ᔕ ∆BDC, suy ra $\frac{AB}{BD}=\frac{BD}{DC}$.

Do đó BD² = AB . DC (đpcm).

Bài 13 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho $\widehat{ADE}=\widehat{ACB}$.

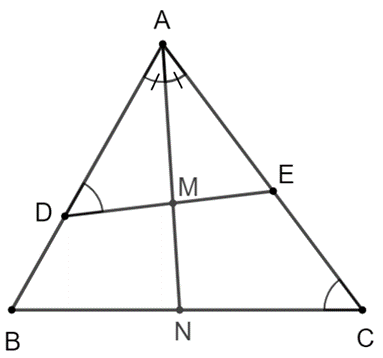
a) Chứng minh rằng ∆AED ᔕ ∆ABC.

b) Tia phân giác của $\widehat{BAC}$ cắt DE tại M và cắt BC tại N.

Chứng minh rằng ME . NC = MD . NB.

Lời giải:

a) Xét ∆AED và ∆ABC có

$\widehat{A}$ chung; $\widehat{ADE}=\widehat{ACB}$.

Do đó ∆AED ᔕ ∆ABC (g.g)

b) Ta có ∆AED ᔕ ∆ABC suy ra $\frac{AE}{AB}=\frac{AD}{AC}$ hay $\frac{AE}{AD}=\frac{AB}{AC}$ (1)

• Vì AM là tia phân giác của $\widehat{DAE}$ nên $\frac{ME}{MD}=\frac{AE}{AD}$ (2)

• Vì AN là tia phân giác của $\widehat{BAC}$ nên $\frac{NB}{NC}=\frac{AB}{AC}$ (3)

Từ (1); (2) và (3) suy ra $\frac{ME}{MD}=\frac{NB}{NC}$ hay ME . NC = MD . NB (đpcm).

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: