Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M

Bài 8 trang 64 SBT Toán 8 Tập 2: Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng:

a) $\frac{CA}{CF}=\frac{ME}{MF}$ và $\frac{BE}{BA}=\frac{ME}{MF}$.

b) ∆BCE ᔕ ∆CFB.

Trả lời

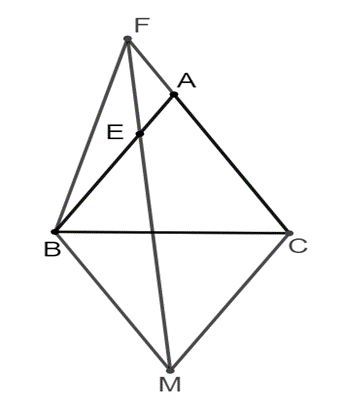
a) Xét ∆MCF có AE // CM (vì AB // CM), theo định lí Thalès ta có:

$\frac{CA}{CF}=\frac{ME}{MF}$ (1)

Xét ∆BEM có AF // BM (vì AC // BM), theo hệ quả của định lí Thalès ta có:

$\frac{AE}{BE}=\frac{EF}{ME}$.

Ta có $\frac{AE}{BE}+1=\frac{EF}{ME}+1$ hay $\frac{AE}{BE}+\frac{BE}{BE}=\frac{EF}{ME}+\frac{ME}{ME}$.

Suy ra $\frac{BA}{BE}=\frac{MF}{ME}$ hay $\frac{BE}{BA}=\frac{ME}{MF}$ (2)

b) Từ (1) và (2), suy ra $\frac{CA}{CF}=\frac{BE}{BA}$, mà AB = BC = AC. Suy ra $\frac{BC}{CF}=\frac{BE}{BC}$.

Xét ∆BCE và ∆CFB có $\frac{BC}{CF}=\frac{BE}{BC}$ và $\widehat{EBC}=\widehat{BCF}$ (∆ABC đều).

Do đó ∆BCE ᔕ ∆CFB (c.g.c).

Trường hợp đồng dạng thứ ba (g.g)

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8