Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho góc ADE = góc ACB

Bài 13 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho $\widehat{ADE}=\widehat{ACB}$.

a) Chứng minh rằng ∆AED ᔕ ∆ABC.

b) Tia phân giác của $\widehat{BAC}$ cắt DE tại M và cắt BC tại N.

Chứng minh rằng ME . NC = MD . NB.

Trả lời

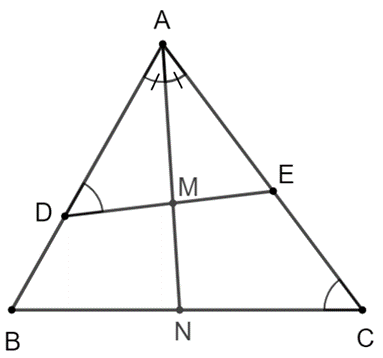
a) Xét ∆AED và ∆ABC có

$\widehat{A}$ chung; $\widehat{ADE}=\widehat{ACB}$.

Do đó ∆AED ᔕ ∆ABC (g.g)

b) Ta có ∆AED ᔕ ∆ABC suy ra $\frac{AE}{AB}=\frac{AD}{AC}$ hay $\frac{AE}{AD}=\frac{AB}{AC}$ (1)

• Vì AM là tia phân giác của $\widehat{DAE}$ nên $\frac{ME}{MD}=\frac{AE}{AD}$ (2)

• Vì AN là tia phân giác của $\widehat{BAC}$ nên $\frac{NB}{NC}=\frac{AB}{AC}$ (3)

Từ (1); (2) và (3) suy ra $\frac{ME}{MD}=\frac{NB}{NC}$ hay ME . NC = MD . NB (đpcm).

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8