a) Tứ giác $EFHD$ là hình gì? Vì sao?

b) Tìm điều kiện của tam giác $ABC$ để tứ giác $EFHD$ là hình vuông.

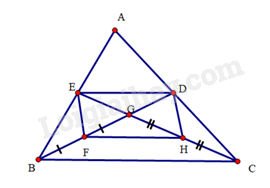
a) Do $G$ là trọng tâm tam giác $ABC$ nên $DG=\frac{1}{2}BG,EG=\frac{1}{2}CG$. Mà $F,H$ lần lượt là trung điểm của $BG,CG$ nên $DG=BF=FG,EG=CH=HG$.

Tứ giác $EFHG$ có hai đường chéo $EH$ và $DF$ cắt nhau tại trung điểm của mỗi đường nên $EFHG$ là hình bình hành.

b) Để hình bình hành $EFHG$ là hình vuông thì $EH=DF$ và $EH\mathrm{\perp }DF$

suy ra $BG=CG,EG=DG$ và $BD\mathrm{\perp }CE$.

$\mathrm{\Delta }BEG=\mathrm{\Delta }CDG$ (c.g.c). Suy ra $BE=CD$. Mà $AB=2BE,AC=2CD$, suy ra $AB=AC$.

Dễ thấy nếu $AB=AC$ và $BD\mathrm{\perp }CE$ thì tứ giác $EFHG$ là hình vuông.

Vậy tam giác $ABC$ cân tại $A$ có đường trung tuyến $BD$, $CE$ vuông góc với nhau thì tứ giác $EFHG$ là hình vuông.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103