Cho hình chữ nhật ABCD có hai cạnh kề không bằng nhau. Tia phân giác của các góc A và B cắt nhau tại E

Bài 32 trang 102 SBT Toán 8 Tập 1: Cho hình chữ nhật $ABCD$ có hai cạnh kề không bằng nhau. Tia phân giác của các góc $A$ và $B$ cắt nhau tại $E$. Tia phân giác của các góc $C$ và $D$ cắt nhau tại $F$. Gọi $G$ là giao điểm của $AE$ và $DF$, $H$ là giao điểm của $BE$ và $CF$. Chứng minh:

a) $GH//CD$

b) Tứ giác $GFHE$ là hình vuông

Trả lời

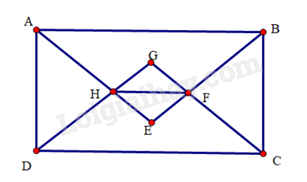
a) Do $ABCD$ là hình chữ nhật nên $\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}={90}^{\circ }$

Mà $AE,BE,CF,DF$ lần lượt là các tia phân giác của các góc $DAB,ABC,BCD,CDA$ 

suy ra $\widehat{DAE}=\widehat{EAB}=\widehat{ABE}=\widehat{EBC}=\widehat{BCF}=\widehat{FCD}=\widehat{CDF}=\widehat{FDA}={45}^{\circ }$

Do đó, các tam giác $EAB,FCD,GAD,HBC$ đều là tam giác vuông cân.

$\mathrm{\Delta }GAD=\mathrm{\Delta }HBC$ (g.c.g). Suy ra $GD=HC$. Mà $FD=FC$, suy ra $FG=FH$.

Do đó, tam giác $FGH$ vuông cân tại $F$. Suy ra $\widehat{FGH}={45}^{\circ }$.

Ta có: $\widehat{FGH}=\widehat{CDF}={45}^{\circ }$ và $\widehat{FGH},\widehat{CDF}$ nằm ở vị trí đồng vị nên $GH//CD$.

b)    $\widehat{EGF}=\widehat{AGD}={90}^{\circ }$ (hai góc đối đỉnh)

Tứ giác $GFHE$ là hình chữ nhật.

Hình chữ nhật $GFHE$ có $FG=FH$ nên $GFHE$ là hình vuông.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103