Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH (Hình 26)

Bài 33 trang 102 SBT Toán 8 Tập 1: Cho hình bình hành $ABCD$. Ở phía ngoài hình bình hành, vẽ các hình vuông $ABEF$ và $ADGH$ (Hình 26). Chứng minh:

a)  $\mathrm{\Delta }AHF=\mathrm{\Delta }ADC$

b)  $AC\mathrm{\perp }HF$.

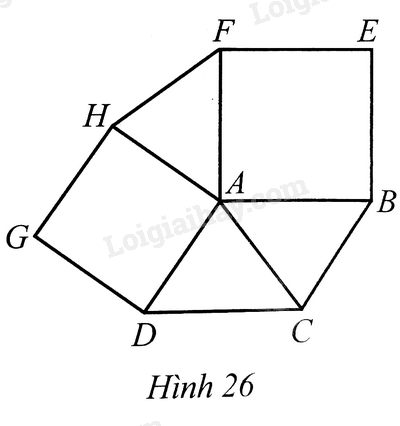
Trả lời

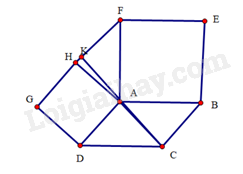
Gọi $K$ là giao điểm của $AC$ và $HF$

a) Do $ABEF$ và $ADGH$ đều là hình vuông nên$\widehat{BAF}=\widehat{DAH}={90}^{\circ },AH=BA,AH=DA$

Do $ABCD$ là hình bình hành nên $BA=DC$. Suy ra $AF=DC$

Ta chứng minh được $\widehat{HAF}+\widehat{DAB}={180}^{\circ }$ và $\widehat{ADC}+\widehat{DAB}={180}^{\circ }$

Suy ra $\widehat{HAF}=\widehat{ADC}$

Xét hai tam giác $HAF$ và $ADC$, ta có: $AH=DA,\widehat{HAF}=\widehat{ADC},AF=DA$

Suy ra $\mathrm{\Delta }HAF=\mathrm{\Delta }ADC$ (c.g.c)

b) Ta có: $\widehat{HAK}+\widehat{DAH}+\widehat{DAC}=\widehat{CAK}={180}^{\circ }$ và $\widehat{DAH}={90}^{\circ }$ nên $\widehat{HAK}+\widehat{DAC}={90}^{\circ }$

Mà $\widehat{AHF}=\widehat{DAC}$ (vì $\mathrm{\Delta }HAF=\mathrm{\Delta }ADC$), suy ra $\widehat{HAK}+\widehat{AHF}={90}^{\circ }$

Trong tam giác $AHK$, ta có: $\widehat{AKH}+\widehat{HAK}+\widehat{AHF}={180}^{\circ }$. Suy ra $\widehat{AKH}={90}^{\circ }$

Vậy $AK\mathrm{\perp }HK$ hai $AC\mathrm{\perp }HF$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103