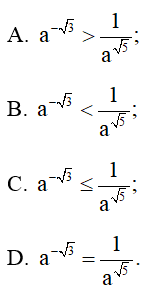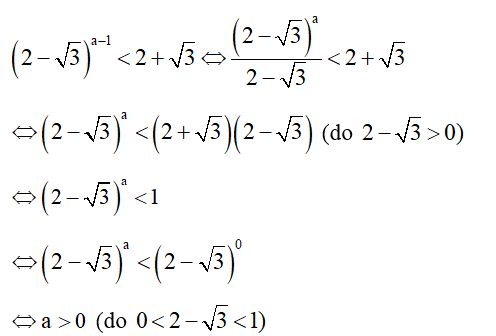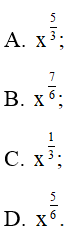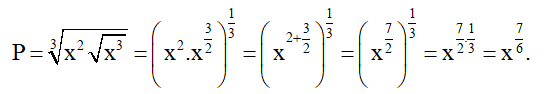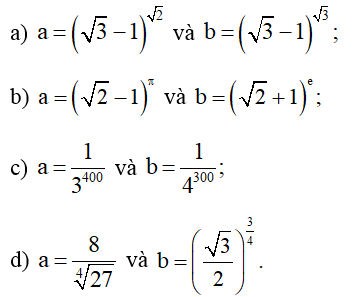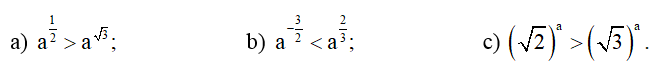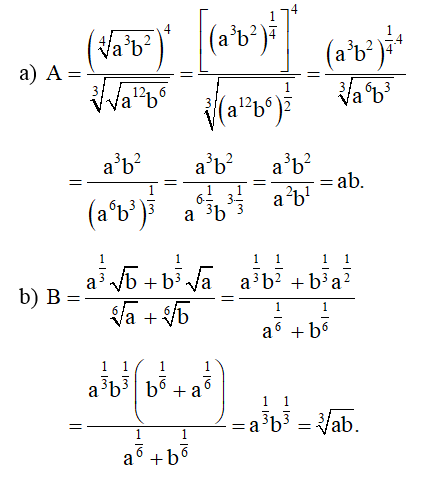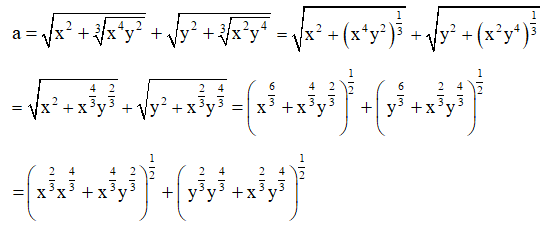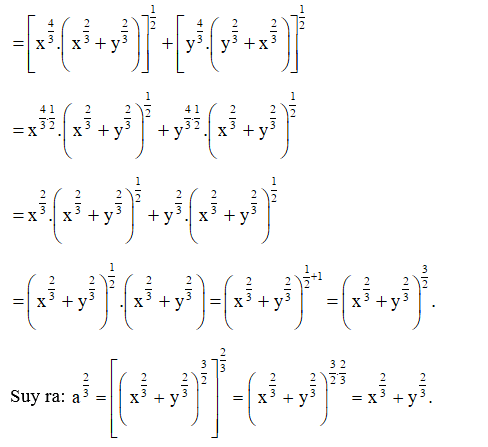Giải SBT Toán 11 (Cánh diều) Bài 1: Phép tính lũy thừa với số mũ thực

Giải SBT Toán 11 Bài 1: Phép tính lũy thừa với số mũ thực

Bài 1 trang 33 SBT Toán 11 Tập 2: Điều kiện xác định của x^–7 là:

A. x ∈ R;

B. x ≠ 0;

C. x ≥ 0;

D. x > 0.

Lời giải:

Đáp án đúng là: B

Từ định nghĩa phép tính lũy thừa với số mũ nguyên: Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0, ta có: $a^{-n}=\frac{1}{a^n}.$

Ta thấy n = 7 ∈ ℕ* nên điều kiện xác định của $x^{-7}=\frac{1}{x^7}$ là x ≠ 0.

Bài 2 trang 34 SBT Toán 11 Tập 2: Điều kiện xác định của $\sqrt[5]{x^3}$ là:

A. x ∈ R;

B. x ≠ 0;

C. x ≥ 0;

D. x > 0.

Lời giải:

Đáp án đúng là: A

Ta thấy n = 5 là số lẻ nên điều kiện xác định của $\sqrt[5]{x^3}$ là x³ ∈ ℝ hay x ∈ ℝ.

Bài 3 trang 34 SBT Toán 11 Tập 2: Điều kiện xác định của $\sqrt[8]{x^3}$ là:

A. x ∈ R;

B. x ≠ 0;

C. x ≥ 0;

D. x > 0.

Lời giải:

Đáp án đúng là: C

Ta thấy n = 8 là số chẵn nên điều kiện xác định của $\sqrt[8]{x^3}$ là x³ ≥ 0 hay x ≥ 0.

Bài 4 trang 34 SBT Toán 11 Tập 2: Điều kiện xác định của $x^{\sqrt{2}}$ là:

A. x ∈ R;

B. x ≠ 0;

C. x ≥ 0;

D. x > 0.

Lời giải:

Đáp án đúng là: D

Ta thấy: $\sqrt{2}$ là số vô tỉ nên điều kiện xác định của $x^{\sqrt{2}}$ là: x > 0.

Bài 5 trang 34 SBT Toán 11 Tập 2: Giá trị của biểu thức $P=2^{1-\sqrt{2}}\cdot 2^{3+\sqrt{2}}\cdot 4^{\frac{1}{2}}$ bằng:

A. 128;

B. 64;

C. 16;

D. 32.

Lời giải:

Đáp án đúng là: D

Ta có:

$P=2^{1-\sqrt{2}}{.2}^{3+\sqrt{2}}{.4}^{\frac{1}{2}}=2^{1-\sqrt{2}+3+\sqrt{2}}.{\left(2^2\right)}^{\frac{1}{2}}$

$=2^4{.2}^{2\cdot \frac{1}{2}}=2^4{.2}^1=2^{4+1}=2^5=32.$

Bài 6 trang 34 SBT Toán 11 Tập 2: Nếu a > 1 thì:

Lời giải:

Đáp án đúng là: A

Do $\sqrt{3}<\sqrt{5}$ và với a > 1 nên $a^{\sqrt{3}}<a^{\sqrt{5}}$ hay $\frac{1}{a^{\sqrt{3}}}>\frac{1}{a^{\sqrt{5}}}.$

Mà $\frac{1}{a^{\sqrt{3}}}=a^{-\sqrt{3}}$ nên $a^{-\sqrt{3}}>\frac{1}{a^{\sqrt{5}}}.$

Bài 7 trang 34 SBT Toán 11 Tập 2: Nếu ${\left(2-\sqrt{3}\right)}^{a-1}<2+\sqrt{3}$ thì:

A. a > 0;

B. a > 1;

C. a < 1;

D. a < 0.

Lời giải:

Đáp án đúng là: A

Ta có:

Bài 8 trang 34 SBT Toán 11 Tập 2: Nếu $a^{\sqrt{3}}<a^{\sqrt{2}}$ thì:

A. a > 1;

B. a < 1;

C. 0 < a < 1;

D. a > 0.

Lời giải:

Đáp án đúng là: C

Vì $a^{\sqrt{3}}<a^{\sqrt{2}}$ và $\sqrt{3}>\sqrt{2}$ suy ra 0 < a < 1.

Vậy nếu $a^{\sqrt{3}}<a^{\sqrt{2}}$ thì 0 < a < 1.

Bài 9 trang 34 SBT Toán 11 Tập 2: Biểu thức $P=\sqrt[3]{x^2\sqrt{x^3}}$ với x > 0 được rút gọn bằng:

Lời giải:

Đáp án đúng là: B

Ta có:

Bài 10 trang 34 SBT Toán 11 Tập 2: Biểu thức $Q=a^{\sqrt{3}}.{\left(\frac{1}{a}\right)}^{\sqrt{3}-1}$với a > 0 được rút gọn bằng:

A. >$\frac{1}{a};$

B. a³;

C. a;

D. 1.

Lời giải:

Đáp án đúng là: C

Ta có: $Q=a^{\sqrt{3}}.{\left(\frac{1}{a}\right)}^{\sqrt{3}-1}=a^{\sqrt{3}}.{\left(a^{-1}\right)}^{\sqrt{3}-1}$

$=a^{\sqrt{3}}.a^{\left(-1\right).\left(\sqrt{3}-1\right)}=a^{\sqrt{3}}.a^{1-\sqrt{3}}=a^{\sqrt{3}+1-\sqrt{3}}=a.$

Bài 11 trang 34 SBT Toán 11 Tập 2: Viết các biểu thức sau về lũy thừa cơ số a, biết:

a) $A=\sqrt[7]{3.\sqrt[5]{\frac{1}{3}}}$ với a = 3;

b) $B=\frac{25\sqrt[3]{5}}{\sqrt{125}}$với $a=\sqrt{5}.$

Lời giải:

a) $A=\sqrt[7]{3.\sqrt[5]{\frac{1}{3}}}=\sqrt[7]{3.\sqrt[5]{3^{-1}}}=\sqrt[7]{{3.3}^{-\frac{1}{5}}}$

$=\sqrt[7]{3^{1-\frac{1}{5}}}=\sqrt[7]{3^{\frac{4}{5}}}=3^{\frac{4}{5}:7}=3^{\frac{4}{5}.\frac{1}{7}}=3^{\frac{4}{35}}.$

Viết biểu thức A về lũy thừa cơ số a = 3 ta được $A=a^{\frac{4}{35}}.$

b) $B=\frac{25\sqrt[3]{5}}{\sqrt{125}}=\frac{5^2\cdot 5^{\frac{1}{3}}}{\sqrt{5^3}}=\frac{5^{2+\frac{1}{3}}}{5^{\frac{3}{2}}}=\frac{5^{\frac{7}{3}}}{5^{\frac{3}{2}}}$

$=5^{\frac{7}{3}-\frac{3}{2}}=5^{\frac{5}{6}}={\left[{\left(\sqrt{5}\right)}^2\right]}^{\frac{5}{6}}={\left(\sqrt{5}\right)}^{2.\frac{5}{6}}={\left(\sqrt{5}\right)}^{\frac{5}{3}}.$

Viết biểu thức B về lũy thừa cơ số $a=\sqrt{5}$ ta được $B=a^{\frac{5}{3}}.$

Bài 12 trang 34 SBT Toán 11 Tập 2: Không sử dụng máy tính cầm tay, so sánh hai số a và b, biết:

Lời giải:

a) Do $0<\sqrt{3}-1<1$ và $\sqrt{2}<\sqrt{3}$ nên ${\left(\sqrt{3}-1\right)}^{\sqrt{2}}>{\left(\sqrt{3}-1\right)}^{\sqrt{3}}.$

Suy ra: a > b.

b) Ta có: $a={\left(\sqrt{2}-1\right)}^{\pi }={\left[\frac{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}{\sqrt{2}+1}\right]}^{\pi }$

$={\left(\frac{2-1}{\sqrt{2}+1}\right)}^{\pi }={\left(\frac{1}{\sqrt{2}+1}\right)}^{\pi }={\left(\sqrt{2}+1\right)}^{-\pi }.$

Do $\sqrt{2}+1>1$ và –π < e nên ta có:

${\left(\sqrt{2}+1\right)}^{-\pi }<{\left(\sqrt{2}+1\right)}^e\iff {\left(\sqrt{2}-1\right)}^{\pi }<{\left(\sqrt{2}+1\right)}^e.$

Suy ra: a < b.

c) Ta có: $a=\frac{1}{3^{400}}={\left(\frac{1}{3^4}\right)}^{100}={\left(\frac{1}{81}\right)}^{100}$ và $b=\frac{1}{4^{300}}={\left(\frac{1}{4^3}\right)}^{100}={\left(\frac{1}{64}\right)}^{100}.$

Do 100 > 0 và $\frac{1}{81}<\frac{1}{64}$ nên ${\left(\frac{1}{81}\right)}^{100}<{\left(\frac{1}{64}\right)}^{100}\iff \frac{1}{3^{400}}<\frac{1}{4^{300}}.$

Suy ra: a < b.

d) Ta có:

$a=\frac{8}{\sqrt[4]{27}}=\frac{2^3}{\sqrt[4]{3^3}}=\frac{{\left(\sqrt[4]{16}\right)}^3}{\sqrt[4]{3^3}}$$=\frac{\sqrt[4]{{16}^3}}{\sqrt[4]{3^3}}=\frac{{16}^{\frac{3}{4}}}{3^{\frac{3}{4}}}={\left(\frac{16}{3}\right)}^{\frac{3}{4}}.$

Do $\frac{16}{3}>\frac{\sqrt{3}}{2}>0$ và $\frac{3}{4}>0$ nên ${\left(\frac{16}{3}\right)}^{\frac{3}{4}}>{\left(\frac{\sqrt{3}}{2}\right)}^{\frac{3}{4}}\iff \frac{8}{\sqrt[4]{27}}>{\left(\frac{\sqrt{3}}{2}\right)}^{\frac{3}{4}}.$

Suy ra: a > b.

Bài 13 trang 35 SBT Toán 11 Tập 2: Xác định các giá trị của số thực a thỏa mãn:

Lời giải:

a) Do $\frac{1}{2}<\sqrt{3}$ nên $a^{\frac{1}{2}}>a^{\sqrt{3}}\iff 0<a<1.$

b) Do $-\frac{3}{2}<\frac{2}{3}$ nên $a^{-\frac{3}{2}}<a^{\frac{2}{3}}\iff a>1.$

c) Do $0<\sqrt{2}<\sqrt{3}$ nên ${\left(\sqrt{2}\right)}^a>{\left(\sqrt{3}\right)}^a\iff a<0.$

Bài 14 trang 35 SBT Toán 11 Tập 2: Cho a > 0, b > 0. Rút gọn mỗi biểu thức sau:

Lời giải:

Bài 15 trang 35 SBT Toán 11 Tập 2: Cho x, y là các số thực dương và số thực a thỏa mãn: $a=\sqrt{x^2+\sqrt[3]{x^4{y}^2}}+\sqrt{y^2+\sqrt[3]{x^2{y}^4}}.$ Chứng minh rằng: $a^{\frac{2}{3}}=x^{\frac{2}{3}}+y^{\frac{2}{3}}.$

Lời giải:

Với x, y > 0 ta có:

Bài 16 trang 35 SBT Toán 11 Tập 2: Một chất phóng xạ có chu kì bán rã là 25 năm, tức là cứ sau 25 năm, khối lượng của chất phóng xạ đó giảm đi một nửa. Giả sử lúc đầu có 10 g chất phóng xạ đó. Viết công thức tính khối lượng của chất đó còn lại sau t năm và tính khối lượng của chất đó còn lại sau 120 năm (làm tròn kết quả đến hàng phần nghìn theo đơn vị gam).

Lời giải:

Chất phóng xạ có chu kì bán rã là T = 25 (năm).

Cứ sau 25 năm, khối lượng của chất phóng xạ đó giảm đi một nửa

Suy ra khối lượng của chất đó còn lại sau t năm là: $m=10.{\left(\frac{1}{2}\right)}^{\frac{t}{25}}$ (g).

Khối lượng của chất đó còn lại sau 120 năm là:

$m=10.{\left(\frac{1}{2}\right)}^{\frac{120}{25}}\approx 0,359$ (g).

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác: