Trong Hình 76, cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng. Chứng minh rằng: AD // BE và BD//CE

Bài 4 trang 96 Toán 7 Tập 2: Trong Hình 76, cho biết các tam giác ABD và BCE là các tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:

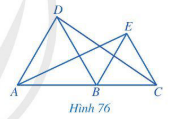
a) AD // BE và BD // CE;

b) $\widehat{ABE}=\widehat{DBC}=120°;$ 

c) AE = CD.

Trả lời

Chứng minh (Hình 76):

a) Vì tam giác ABD đều (giả thiết)

Nên AB = BD = AD và $\widehat{DAB}=\widehat{DBA}=\widehat{ADB}=60°$ 

Tam giác BCE đều (giả thiết)

Nên BC = CE = BE và $\widehat{ECB}=\widehat{EBC}=\widehat{CEB}=60°$ 

Vì $\widehat{DAB}=\widehat{EBC}\left(=60°\right)$ mà hai góc này ở vị trí đồng vị

Nên AD // BE (dấu hiệu nhận biết hai đường thẳng song song)

Vì $\widehat{DBA}=\widehat{ECB}\left(=60°\right)$ mà hai góc này ở vị trí đồng vị

Nên BD // CE (dấu hiệu nhận biết hai đường thẳng song song)

Vậy AD // BE và BD // CE.

b) Vì $\widehat{ABE}$ và $\widehat{EBC}$ là hai góc kề bù nên $\widehat{ABE}+\widehat{EBC}=180°$ (tính chất hai góc kề bù)

Suy ra $\widehat{ABE}=180°-\widehat{EBC}=180°-60°=120°$

Tương tự ta cũng có $\widehat{DBA}+\widehat{DBC}=180°$ (tính chất hai góc kề bù)

Nên $\widehat{DBC}=180°-\widehat{DBA}=180°-60°=120°$

Vậy $\widehat{ABE}=\widehat{DBC}=120°.$

c) Xét tam giác ABE và tam giác DBC có:

AB = DB (chứng minh trên)

$\widehat{ABE}=\widehat{DBC}\left(=120°\right)$ (chứng minh trên)

BE = BC (chứng minh trên)

Do đó $∆$ABE = $∆$DBC (c.g.c)

Suy ra AE = CD (hai cạnh tương ứng)

Vậy AE = CD.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân

Bài 8: Đường vuông góc và đường xiên

Bài 9: Đường trung trực của một đoạn thẳng

Bài 10: Tính chất ba đường trung tuyến của tam giác