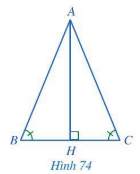
Cho tam giác ABC thoả mãn . Kẻ AH vuông góc với BC, H thuộc BC (Hình 74). Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao
438
16/11/2023
Hoạt động 3 trang 94 Toán 7 Tập 2: Cho tam giác ABC thoả mãn . Kẻ AH vuông góc với BC, H thuộc BC (Hình 74).
a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?
b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?
Trả lời
a) Vì AH ⊥ BC (H ∈ BC) nên
Do đó tam giác ABH vuông tại H, tam giác ACH vuông tại H
Xét tam giác ABH vuông tại H có: (trong tam giác vuông, hai góc nhọn phụ nhau)
Tam giác ACH vuông tại H có: (trong tam giác vuông, hai góc nhọn phụ nhau)
Mà (giả thiết)
Do đó
Xét tam giác ABH (vuông tại H) và tam giác ACH (vuông tại H) có:
AH là cạnh chung
Do đó ABH = ACH (cạnh góc vuông – góc nhọn kề)
Vậy ABH = DACH.
b) Vì ABH = ACH (chứng minh câu a)
Suy ra AB = AC (hai cạnh tương ứng)
Vậy AB = AC.
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
Bài 7: Tam giác cân
Bài 8: Đường vuông góc và đường xiên
Bài 9: Đường trung trực của một đoạn thẳng
Bài 10: Tính chất ba đường trung tuyến của tam giác

