Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi

Bài 4 trang 78 Toán lớp 10 Tập 1: Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).

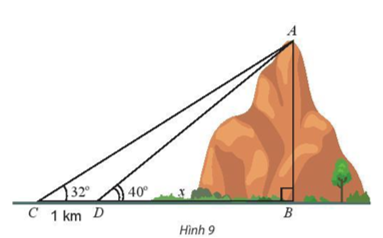
Trả lời

Vì $\widehat{CDA}$ và $\widehat{ADB}$ là hai góc kề bù nên $\widehat{CDA}={180}^0-{40}^0={140}^0$

Xét tam giác ACD có : $\widehat{CAD}={180}^0-({32}^0+{140}^0)=8^0$

Áp dụng định lí sin ta có: $\frac{AD}{\sin C}=\frac{CD}{\sin A}\Rightarrow AD=\frac{CD.\sin C}{\sin A}=\frac{1.\sin {32}^0}{\sin 8^0}$ ≈ 3,81 km.

Xét tam giác ABD vuông tại B, ta có:$\sin \widehat{ADB}=\frac{AB}{AD}\Rightarrow AB=AD.\sin {40}^0$ ≈ 2,45 km.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ