Tìm giới hạn của các dãy số sau: a) un = n^2 / (3n^2+7n-2) 

Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau:

a) $u_n=\frac{n^2}{3n^2+7n-2}$;

b) $v_n=\sum _{k=0}^n\frac{3^k+5^k}{6^k}$;

c) ${\text{w}}_n=\frac{\sin n}{4n}$.

Trả lời

a) $u_n=\frac{n^2}{3n^2+7n-2}$

Ta có: $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\frac{n^2}{3n^2+7n-2}$$=\underset{n\to +\infty }{\lim }\frac{n^2}{n^2\left(3+\frac{7}{n}-\frac{2}{n^2}\right)}$$=\underset{n\to +\infty }{\lim }\frac{1}{3+\frac{7}{n}-\frac{2}{n^2}}=\frac{1}{3}$

b) $v_n=\sum _{k=0}^n\frac{3^k+5^k}{6^k}$$=\frac{3^0+5^0}{6^0}+\frac{3^1+5^1}{6^1}+\frac{3^2+5^2}{6^2}+\mathrm{...}+\frac{3^n+5^n}{6^n}$

$=\left(\frac{3^0}{6^0}+\frac{5^0}{6^0}\right)+\left(\frac{3^1}{6^1}+\frac{5^1}{6^1}\right)+\left(\frac{3^2}{6^2}+\frac{5^2}{6^2}\right)+\mathrm{...}+\left(\frac{3^n}{6^n}+\frac{5^n}{6^n}\right)$

$=\left({\left(\frac{1}{2}\right)}^0+{\left(\frac{5}{6}\right)}^0\right)+\left({\left(\frac{1}{2}\right)}^1+{\left(\frac{5}{6}\right)}^1\right)+\left({\left(\frac{1}{2}\right)}^2+{\left(\frac{5}{6}\right)}^2\right)+\mathrm{...}+\left({\left(\frac{1}{2}\right)}^n+{\left(\frac{5}{6}\right)}^n\right)$

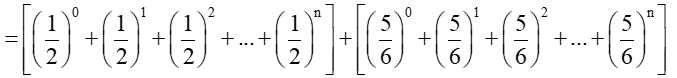
Vì ${\left(\frac{1}{2}\right)}^1+{\left(\frac{1}{2}\right)}^2+\mathrm{...}+{\left(\frac{1}{2}\right)}^n$ là tổng n số hạng đầu của cấp số nhân với số hạng đầu là ${\left(\frac{1}{2}\right)}^1=\frac{1}{2}$ và công bội là $\frac{1}{2}$ nên

${\left(\frac{1}{2}\right)}^0+{\left(\frac{1}{2}\right)}^1+{\left(\frac{1}{2}\right)}^2+\mathrm{...}+{\left(\frac{1}{2}\right)}^n={\left(\frac{1}{2}\right)}^0+\frac{\frac{1}{2}\left(1-{\left(\frac{1}{2}\right)}^n\right)}{1-\frac{1}{2}}$$=1+\left(1-{\left(\frac{1}{2}\right)}^n\right)=2-{\left(\frac{1}{2}\right)}^n$.

Tương tự, ta tính được:

${\left(\frac{5}{6}\right)}^0+{\left(\frac{5}{6}\right)}^1+{\left(\frac{5}{6}\right)}^2+\mathrm{...}+{\left(\frac{5}{6}\right)}^n={\left(\frac{5}{6}\right)}^0+\frac{\frac{5}{6}\left(1-{\left(\frac{5}{6}\right)}^n\right)}{1-\frac{5}{6}}$$=1+5\left(1-{\left(\frac{5}{6}\right)}^n\right)=6-5\cdot {\left(\frac{5}{6}\right)}^n$.

Do đó,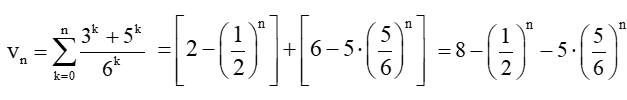 

Vậy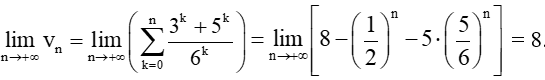 

c) ${\text{w}}_n=\frac{\sin n}{4n}$

Ta có: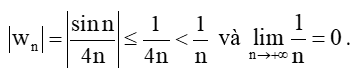 

Do đó, $\underset{n\to +\infty }{\lim }{\text{w}}_n=\underset{n\to +\infty }{\lim }\frac{\sin n}{4n}=0$.

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Một vài áp dụng của toán học trong tài chính

Lực căng mặt ngoài của nước