Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, góc BAC = α . Kẻ đường kính BD của đường tròn (O). Cho α là góc nhọn
413
08/06/2023
Hoạt động 9 trang 69 Toán lớp 10 Tập 1: Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, ^BAC=α. Kẻ đường kính BD của đường tròn (O). Cho α là góc nhọn. Chứng minh:
a) ^BDC=α;
b) asinα=2R.
Trả lời
Do α là góc nhọn ta vẽ được hình như sau:
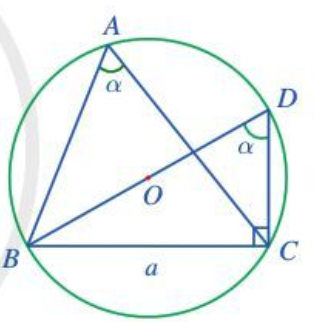
a) Trong đường tròn (O) ta có ^BAC=^BDC (2 góc nội tiếp cùng chắn cung nhỏ BC).
Vậy ^BDC=α.
b) Do ^BCD là góc nội tiếp chắn nửa đường tròn (O) nên ^BCD=90°.
Khi đó là tam giác vuông tại C.
Xét trong tam giác BCD vuông tại C có hay .
Do đó .
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài tập cuối chương 3
Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 3: Khái niệm vectơ
Bài 4: Tổng và hiệu của hai vectơ

