Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, góc BAC = α. Cho α là góc vuông. Kẻ đường kính BD của đường tròn (O)
422
08/06/2023
Hoạt động 11 trang 70 Toán lớp 10 Tập 1: Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R và có BC = a, ^BAC=α. Kẻ đường kính BD của đường tròn (O). Cho α là góc vuông. Chứng minh: asinα=2R.
Trả lời
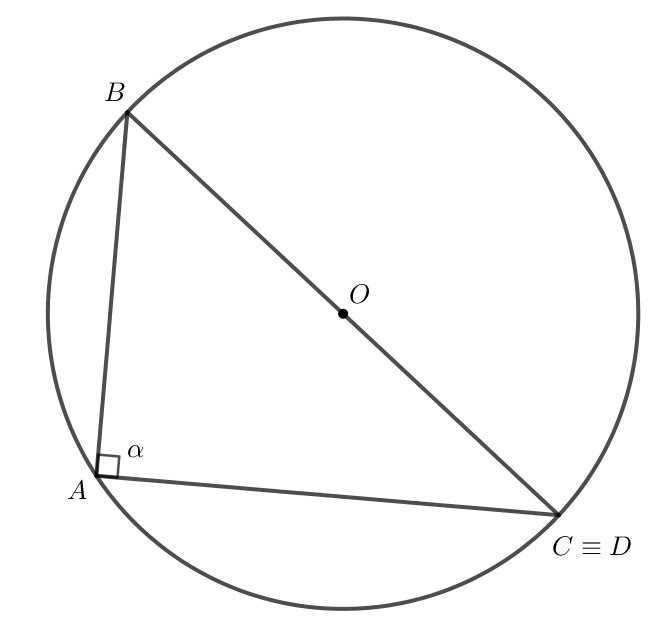
Do ^BAC=α=90° và là góc nội tiếp trong đường tròn (O) nên là góc nội tiếp chắn nửa đường tròn.
Do đó BC là đường kính của đường tròn (O).
Mà BD là đường kính của đường tròn (O) nên C  D.
D.
Do α = 90o nên sin α = sin 90o = 1.
Do BC là đường kính của đường tròn (O; R) nên BC = 2R hay a = 2R.
Do đó hay .
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài tập cuối chương 3
Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 3: Khái niệm vectơ
Bài 4: Tổng và hiệu của hai vectơ

