Cho tam giác ABC có BC = a, AC = b, góc BAC = α . Kẻ đường cao BH. Cho α là góc vuông
Hoạt động 8 trang 68 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, ^BAC=α. Kẻ đường cao BH.
Cho α là góc vuông. Chứng minh a2 = b2 + c2 – 2bc cos α.
Hoạt động 8 trang 68 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, ^BAC=α. Kẻ đường cao BH.
Cho α là góc vuông. Chứng minh a2 = b2 + c2 – 2bc cos α.
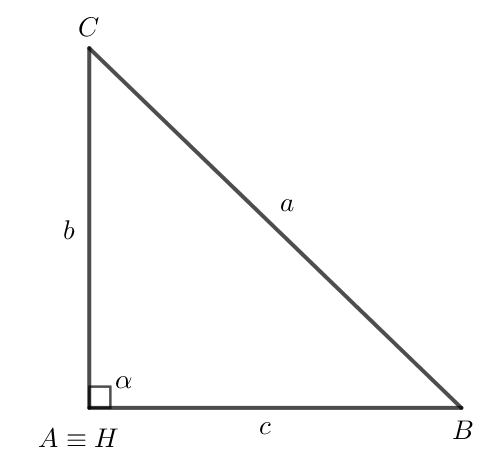
Do α = 90° nên tam giác ABC vuông tại A và cos α = cos 90o = 0.
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 = b2 + c2 - 0 = b2 + c2 - 2bc.cos α.
Vậy a2 = b2 + c2 – 2bc.cos α.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 5: Hai dạng phương trình quy về phương trình bậc hai