Giải SBT Toán 8 Bài 3: Hình thang cân
Lời giải:
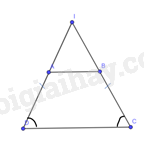
Gọi I là giao điểm của AD và BC
Do ˆC=ˆD nên tam giác ICD cân tại I. Suy ra ID=IC
Mà AD=BC, suy ra IA=IB. Do đó, tam giác IAB cân tại I.
Vì hai tam giác IAB và ICD đều cân tại I nên
^IAB=ˆD (cùng bằng 180∘−ˆI2)
Mà ^IAB và ˆD nằm ở vị trí đồng vị, suy ra AB//CD
Tứ giác ABCD có AB//CD và ˆC=ˆD nên ABCD là hình thang cân.
Lời giải:
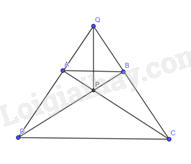
ΔACD=ΔBDC (c.g.c). Suy ra ^PCD=^PDC
Do đó, tam giác PCD cân tại P. Suy ra PC=PD
Mà AC=BD, suy ra PA=PB
Do AB//CD nên ^QAB=^ADC;^QBA=^BCD (các cặp góc đồng vị)
Mặt khác, ^ADC=^BCD nên ^QAB=^QBA
Do đó, tam giác QAB cân tại Q. Suy ra QA=QB
Mà AD=BC, suy ra QD=QC
Ta có: PA=PB,PC=PD và QA=QB,QC=QD nên PQ là đường trung trực của cả hai đoạn thẳng AB và CD.
Lời giải:
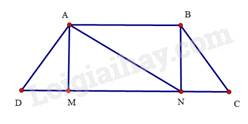
ΔADM=ΔBCN (cạnh huyền – góc nhọn)
Suy ra AM=BN;DM=CN
ΔABN=ΔNMA (cạnh huyền – góc nhọn)
Suy ra AB=NM. Do đó, NM=3cm
Ta có: DM+NM+CN=CD và DM=CN nên 2DM+3=6
Suy ra DM=1,5
Mà DN=DM+NM, suy ra DN=4,5cm
Trong tam giác ADM vuông tại M, ta có: AD2=AM2+DM2
Suy ra AM2=AD2−DM2=4. Vậy AM=√4=2(cm).
a) Chứng minh tứ giác BMNC là hình thang cân
b) Xác định vị trí các điểm M,N để BM=MN=NC.
Lời giải:
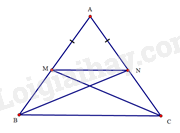
a) Vì hai tam giác AMN và ABC đều cân tại A nên
^AMN=^ABC (cùng bằng 180∘−ˆA2)
Mà ^AMN và ^ABC nằm ở vị trí đồng vị, suy ra MN//BC.
Tứ giác BMNC có MN//BC và ^MBC=^NCB nên BMNC là hình thang cân.
b) Do BM=MN nên tam giác MBN cân tại M. Suy ra ^MNB=^MBN. Mà ^MNB=^NBC (hai góc so le trong), suy ra ^MBN=^NBC. Do đó, BN là tia phân giác của góc ABC.
Chứng minh tương tự ta được CM là tia phân giác của góc ACB.
Dễ thấy, nếu các điểm M,N được xác định sao cho BM,CN lần lượt là tia phân giác của góc ABC,ACB thì BN=MN=CN.
Vậy M là giao điểm của AB và tia phân giác của góc ACB,N là giao điểm của AC và tia phân giác của góc ABC thì BN=MN=CN.
a) Tứ giác BCDE là hình gì? Vì sao?
b) Tính độ dài đoạn thẳng CD (làm tròn kết quả đến hàng phần mười của centimet).
Lời giải:
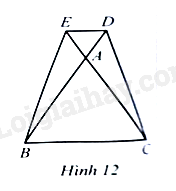
a) Tam giác đều ABC có AB=BC=AC=6cm; ^BAC=^CBA=^ACB=60∘
Ta có: ^DAE=^BAC (hai góc đối đỉnh) nên ^DAE=60∘
Tam giác ADE có AD=AE và ^DAE=60∘ nên ADE là tam giác đều. Suy ra ^ADE=60∘. Do đó ^CBA=^ADE (vì cùng bằng 60∘). Mà ^CBA và ^ADE nằm ở vị trí so le trong, suy ra BC//DE.
Ta có: AB=AC và AD=AE nên BD=CE.
Tứ giác BCDE có BC//DE và BD=CE nên BCDE là hình thang cân.
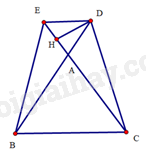
b) Kẻ DH vuông góc với CE tại H.
ΔADH=ΔEDH (cạnh huyền – cạnh góc vuông)
Suy ra AH=EH=AE2=1cm
Trong tam giác ADH vuông tại H, ta có: CD2=CH2+DH2. Suy ra CD2=52
Vậy CD=√52≈7,2(cm).
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:




