Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB

Bài 10 trang 103 Toán lớp 10 Tập 1: Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng $\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{3}{2}\overrightarrow{MO}$.

Trả lời

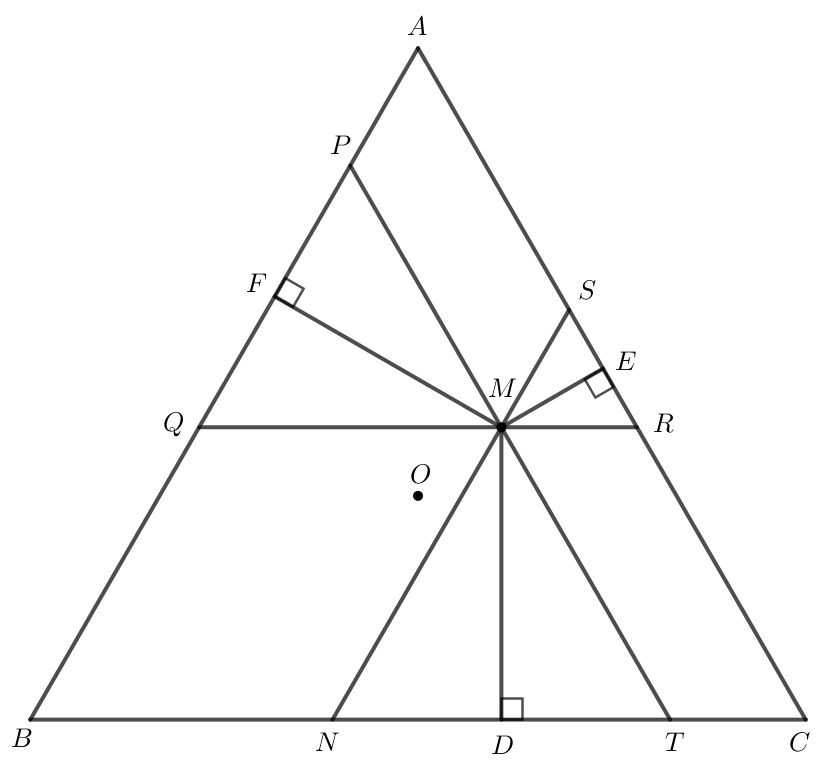
Tam giác ABC đều nên $\widehat{ABC}=\widehat{ACB}=\widehat{BAC}=60°$.

Qua M kẻ NS // AB, PT // AC, RQ // BC.

Do NS //AB nên $\widehat{MNT}=\widehat{ABC}=60°$ và $\widehat{M\text{SR}}=\widehat{BAC}=60°$.

Do PT // AC nên $\widehat{MTN}=\widehat{ACB}=60°$ và $\widehat{MPQ}=\widehat{BAC}=60°$.

Do RQ // BC nên $\widehat{M\text{RS}}=\widehat{ACB}=60°$ và $\widehat{MQP}=\widehat{ABC}=60°$.

Khi đó các tam giác MNT, MRS và MPQ là các tam giác đều.

Tam giác MNT đều có MD $\perp$ NT nên D là trung điểm của NT.

Tam giác MRS đều có ME $\perp$ RS nên E là trung điểm của RS.

Tam giác MPQ đều có MF $\perp$PQ nên F là trung điểm của PQ.

Do D là trung điểm của NT nên $\overrightarrow{MN}+\overrightarrow{MT}=2\overrightarrow{M\text{D}}$.

Do E là trung điểm của RS nên $\overrightarrow{MR}+\overrightarrow{MS}=2\overrightarrow{ME}$.

Do F là trung điểm của PQ nên $\overrightarrow{MP}+\overrightarrow{MQ}=2\overrightarrow{MF}$.

Do đó $2\overrightarrow{M\text{D}}+2\overrightarrow{ME}+2\overrightarrow{MF}=\overrightarrow{MN}+\overrightarrow{MT}+\overrightarrow{MR}+\overrightarrow{MS}+\overrightarrow{M\text{P}}+\overrightarrow{MQ}$

$=\left(\overrightarrow{MN}+\overrightarrow{MQ}\right)+\left(\overrightarrow{MT}+\overrightarrow{MR}\right)+\left(\overrightarrow{MS}+\overrightarrow{M\text{P}}\right)$

Tứ giác MNBQ có MN // BQ và MQ // BN nên MNBQ là hình bình hành.

Tứ giác MTCR có MT // CR và MR // CT nên MTCR là hình bình hành.

Tứ giác MSAP có MP // AS và MS // AP nên MSAP là hình bình hành.

Khi đó áp dụng quy tắc hình bình hành ta có:

$\overrightarrow{MN}+\overrightarrow{MQ}=\overrightarrow{MB}$; $\overrightarrow{MT}+\overrightarrow{MR}=\overrightarrow{MC}$; $\overrightarrow{MS}+\overrightarrow{M\text{P}}=\overrightarrow{MA}$.

Do đó $\left(\overrightarrow{MN}+\overrightarrow{MQ}\right)+\left(\overrightarrow{MT}+\overrightarrow{MR}\right)+\left(\overrightarrow{MS}+\overrightarrow{M\text{P}}\right)=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$.

Do O là trọng tâm của tam giác ABC nên $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}$ hay

$2\overrightarrow{M\text{D}}+2\overrightarrow{ME}+2\overrightarrow{MF}=3\overrightarrow{MO}$.

Do đó $\overrightarrow{M\text{D}}+\overrightarrow{ME}+\overrightarrow{MF}=\frac{3}{2}\overrightarrow{MO}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu