Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng vectơ RJ + vectơ IQ + vectơ PS = vectơ 0
802
12/06/2023
Bài 8 trang 103 Toán lớp 10 Tập 1: Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng →RJ+→IQ+→PS=→0.
Trả lời
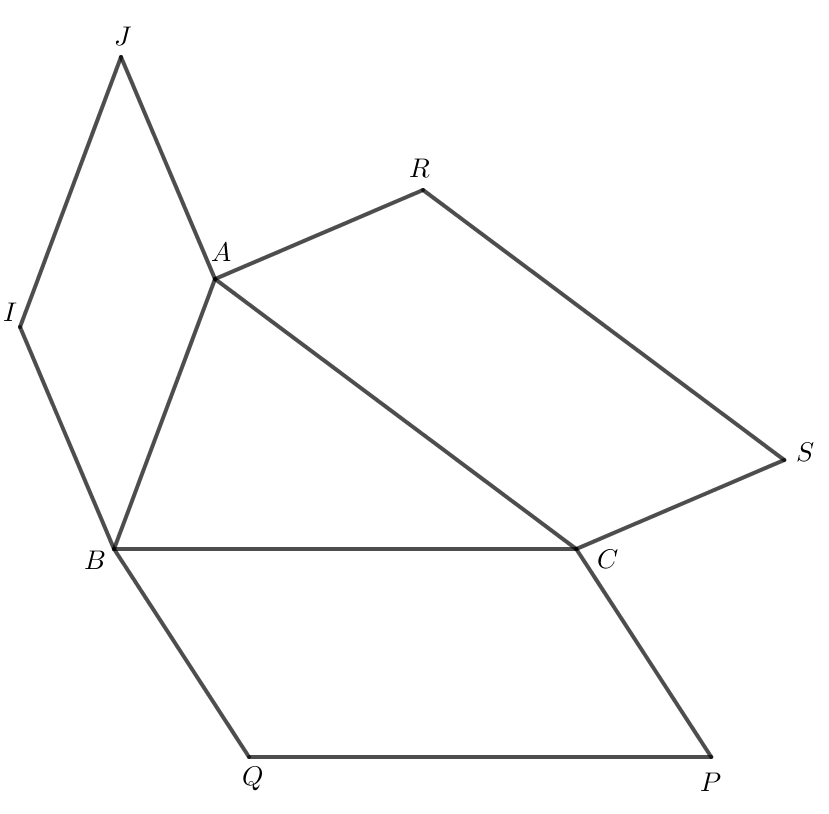
Ta có →RJ+→IQ+→PS=→RA+→AJ+→IB+→BQ+→PC+→CS.
Do ABIJ là hình bình hành nên →AJ=−→IB.
Do CARS là hình bình hành nên →RA=−→CS.
Do BCPQ là hình bình hành nên →BQ=−→PC.
Do đó →RA+→AJ+→IB+→BQ+→PC+→CS=−→CS−→IB+→IB−→PC+→PC+→CS
=(−→CS+→CS)+(−→IB+→IB)+(−→PC+→PC)=→0.
Vậy →RJ+→IQ+→PS=→0.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ
Bài 4: Tích vô hướng của hai vectơ
Bài tập cuối chương 5
Bài 1: Số gần đúng và sai số
Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

