Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho vectơ CE = vectơ AN (Hình 1)
617
12/06/2023
Bài 4 trang 102 Toán lớp 10 Tập 1: Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho →CE=→AN (Hình 1).
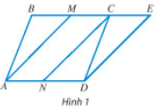
a) Tìm tổng của các vectơ →NC và →MC; →AM và →CD; →AD và →NC.
b) Tìm các vectơ hiệu: →NC−→MC; →AC−→BC; →AB−→ME.
c) Chứng minh →AM+→AN=→AB+→AD.
Trả lời
M là trung điểm của BC nên BM = MC = 12BC.
N là trung điểm của AD nên AN = ND = 12AD.
Do ABCD là hình bình hành nên BC = AD.
Do đó BM = MC = AN = ND.
Do →CE=→AN nên CE = AN.
Do đó BM = MC = AN = ND = CE.
Khi đó ta có AMCN, NCED là các hình bình hành.
a) +) Tính →NC+→MC:
Ta có →MC=→CE nên →NC+→MC=→NC+→CE=→NE.
+) Tính →AM+→CD:
Ta có →AM=→NC nên →AM+→CD=→NC+→CD=→ND.
+) Tính →AD+→NC:
Ta có →NC=→AM nên →AD+→NC=→AD+→AM=→AE.
b) +) Tính →NC−→MC:
Ta có →NC−→MC=→NM.
+) Tính →AC−→BC:
Ta có →AC−→BC=→AB.
+) Tính →AB−→ME:
Ta có →ME=→AD nên →AB−→ME=→AB−→AD=→DB.
c) Ta có →AM+→AN=→AC và →AB+→AD=→AC.
Do đó →AM+→AN=→AB+→AD.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ
Bài 4: Tích vô hướng của hai vectơ
Bài tập cuối chương 5
Bài 1: Số gần đúng và sai số
Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

