Bài 7 trang 103 Toán lớp 10 Tập 1: Cho bốn điểm A, B, C, D. Chứng minh rằng khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Phần thuận: thì trung điểm hai đoạn thẳng AD và BC trùng nhau.
Do nên hai vectơ , cùng hướng và AB = CD.
Do hai vectơ , cùng hướng nên ta có 2 trường hợp:
Trường hợp 1. Đường thẳng AB và CD trùng nhau, lại có AB = CD nên trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Trường hợp 2. Đường thẳng AB và CD song song với nhau.
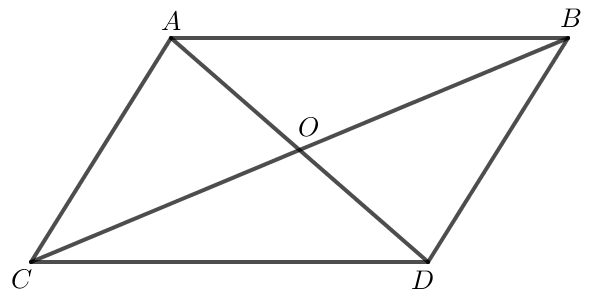
Đường thẳng AB và CD song song với nhau, lại có AB = CD nên ABDC là hình bình hành.
Khi đó tâm O của hình bình hành ABCD là giao điểm hai đường chéo AD và BC nên O là trung điểm của AD và BC tức trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Phần đảo: Trung điểm của hai đoạn thẳng AD và BC trùng nhau thì .
Trường hợp 1. Hai đường thẳng AD và BC trùng nhau.
Gọi trung điểm của AD và BC là O.
Do O là trung điểm của AD nên OA = OD.
Do O là trung điểm của BC nên OB = OC.
Do đó OB - OA = OC - OD hay AB = CD.
Ta thấy hai vectơ và cùng hướng và AB = CD nên .
Trường hợp 2. Hai đường thẳng AD và BC cắt nhau.
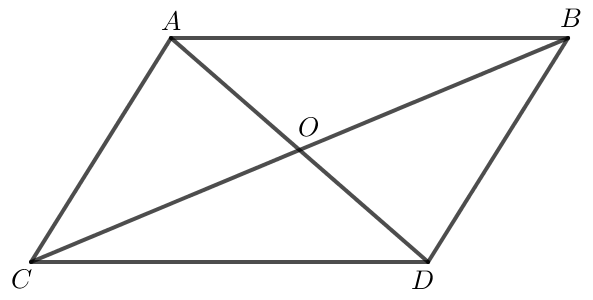
Hai đường thẳng AD và BC cắt nhau tại điểm O, điểm O là trung điểm của AD và BC nên ABDC là hình bình hành.
Do đó AB // CD và AB = CD.
Ta thấy hai vectơ và cùng hướng và AB = CD nên .
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ
Bài 4: Tích vô hướng của hai vectơ