Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng

Bài 9.45 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB). Chứng minh rằng:

a) ∆ABC ᔕ ∆HAC và CA² = CH . CB.

b) $\frac{AH}{BC}=\frac{HE}{AB}$ .

Trả lời

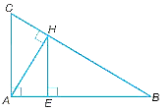
a) Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

 chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AC}{HC}=\frac{BC}{AC}$  nên AC² = CH . BC.

b)

Vì HE vuông góc với AB (E thuộc AB) nên $\widehat{AEH}=90°$  .

Ta có $\widehat{HAE}+\widehat{CAH}=\widehat{CAB}=90°$  và $\widehat{C}+\widehat{CAH}=90°$  (do tam giác CAH vuông tại H).

Do đó, $\widehat{HAE}=\widehat{C}$  (cùng phụ với góc CAH).

Tam giác AHE vuông ở E và tam giác CBA vuông ở A có:

$\widehat{HAE}=\widehat{C}$

Do đó, ∆AHE ᔕ ∆CBA (hai góc nhọn bằng nhau).

Suy ra: $\frac{AH}{BC}=\frac{HE}{AB}$ .

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: