Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'. Chứng minh rằng

Bài 9.52 trang 64 SBT Toán lớp 8 Tập 2: Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'. Chứng minh rằng:

a) BC² + 3BA² = 4BM² và B'C'² + 3B'A'² = 4B'M'²;

b) Nếu $\frac{BC}{BM}=\frac{B\text{'}C\text{'}}{B\text{'}M\text{'}}$  thì ∆ABC ᔕ ∆A'B'C'.

Trả lời

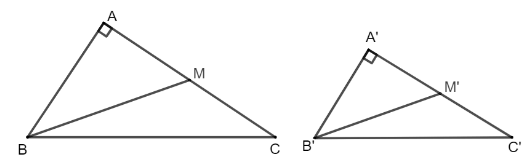
a) Vì M là trung điểm của AC nên AC = 2AM. Suy ra AC² = (2AM)² = 4AM².

Áp dụng định lý Pythagore cho tam giác ABC vuông tại A có:

BC² = AB² + AC².

Áp dụng định lý Pythagore cho tam giác ABM vuông tại A có:

BM² = AB² + AM².

Do đó, 4BM² = 4(AB² + AM²) = 4AB² + 4AM² = 4AB² + AC²

= 3AB² + (AB² + AC²) = 3AB² + BC².

Vậy BC² + 3BA² = 4BM².

Vì M' là trung điểm của A'C' nên A'C' = 2A'M'. Suy ra A'C'² = (2A'M')² = 4A'M'².

Áp dụng định lí Pythagore cho tam giác A'B'C' vuông tại A' có:

B'C'² = A'B'² + A'C'².

Áp dụng định lý Pythagore cho tam giác A'B'M' vuông tại A' có:

B'M'² = A'B'² + A'M'².

Do đó, 4B'M'² = 4(A'B'² + A'M'²) = 4A'B'² + 4A'M'²  = 4A'B'² + A'C'²

= 3A'B'² + (A'B'² + A'C'²) = 3A'B'² + B'C'².

Vậy B'C'² + 3B'A'² = 4B'M'².

b) Giả sử $\frac{BC}{BM}=\frac{B\text{'}C\text{'}}{B\text{'}M\text{'}}$ . Suy ra $\frac{B{C}^2}{B{M}^2}=\frac{B\text{'}C{\text{'}}^2}{B\text{'}M{\text{'}}^2}$  (1).

Theo phần a ta có: BC² + 3BA² = 4BM², chia cả 2 vế cho BM², ta được:

$\frac{B{C}^2}{B{M}^2}+3\frac{B{A}^2}{B{M}^2}=4$.

Tương tự, ta có $\frac{B\text{'}C{\text{'}}^2}{B\text{'}M{\text{'}}^2}+3\frac{B\text{'}A{\text{'}}^2}{B\text{'}M{\text{'}}^2}=4$ .

Do đó, $\frac{B{C}^2}{B{M}^2}+3\frac{B{A}^2}{B{M}^2}=\frac{B\text{'}C{\text{'}}^2}{B\text{'}M{\text{'}}^2}+3\frac{B\text{'}A{\text{'}}^2}{B\text{'}M{\text{'}}^2}\left(=4\right)$       (2).

Từ (1) và (2), suy ra: $\frac{B{A}^2}{B{M}^2}=\frac{B\text{'}A{\text{'}}^2}{B\text{'}M{\text{'}}^2}$  hay $\frac{BA}{BM}=\frac{B\text{'}A\text{'}}{B\text{'}M\text{'}}$ .

Do đó, $\frac{BC}{B\text{'}C\text{'}}=\frac{BM}{B\text{'}M\text{'}}=\frac{BA}{B\text{'}A\text{'}}$.

Hai tam giác ABC vuông tại A và A'B'C' vuông tại A' có $\frac{BC}{B\text{'}C\text{'}}=\frac{BA}{B\text{'}A\text{'}}$ .

Vậy ∆ABC ᔕ ∆A'B'C' (ch – cgv).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: