Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng

Bài 9.51 trang 64 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:

a) AM . AB = AH² và AM . AB = AN . AC.

b) ∆AMN ᔕ ∆ACB.

Trả lời

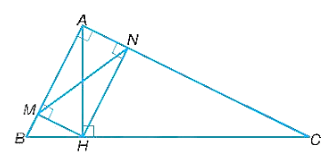
a) Tam giác AMH vuông ở M và tam giác AHB vuông ở H có:

 $\widehat{HAB}$ chung

Do đó, ∆AMH ᔕ ∆AHB (góc nhọn).

Suy ra $\frac{AM}{AH}=\frac{AH}{AB}$  nên AM . AB = AH² (1).

Tam giác ANH vuông ở N và tam giác AHC vuông ở H có:

$\widehat{HAC}$ chung

Do đó, ∆ANH ᔕ ∆AHC (góc nhọn).

Suy ra $\frac{AN}{AH}=\frac{AH}{AC}$  nên AN . AC = AH² (2).

Từ (1) và (2) ta có: AM . AB = AN . AC.

b) Theo phần a ta có: AM . AB = AN . AC nên $\frac{AM}{AC}=\frac{AN}{AB}$ .

Tam giác AMN và tam giác ACB có:

$\widehat{BAC}$ chung $\frac{AM}{AC}=\frac{AN}{AB}$

Do đó, ∆AMN ᔕ ∆ACB (c.g.c).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: