Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN

Bài 9.53 trang 64 SBT Toán lớp 8 Tập 2: Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN.

a) Chứng minh rằng CM ⊥ DN.

b) Biết AB = 4 cm, hãy tính diện tích tam giác ONC.

Trả lời

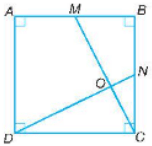
a) Vì ABCD là hình vuông nên AB = BC = CD = DA;

và $\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90°$ .

Vì M là trung điểm của AB nên AM = MB = $\frac{1}{2}$ AB.

Vì N là trung điểm của BC nên NB = NC = $\frac{1}{2}$ BC.

Mà AB = BC nên AM = MB = NB = NC.

Xét tam giác CBM vuông ở B và tam giác DCN vuông ở C có:

MB = NC (cmt)

BC = CD (cmt)

Do đó, tam giác CBM và tam giác DCN bằng nhau (hai cạnh góc vuông).

Suy ra $\widehat{BMC}=\widehat{DNC}$ .

Mà $\widehat{BMC}+\widehat{MCB}=90°$  nên $\widehat{DNC}+\widehat{MCB}=90°$ .

Tam giác CON có:

 $\widehat{ONC}+\widehat{OCN}=90°$ (do $\widehat{DNC}+\widehat{MCB}=90°$ ).

Nên $\widehat{NOC}=90°$ .

Do đó, CM vuông góc với DN tại O.

b) Ta có BC = CD = DA = AB = 4 cm; NC = $\frac{1}{2}$ BC = $\frac{1}{2}$ CD = 2 cm hay CD = 2NC.

Áp dụng định lý Pythagore vào tam giác CND vuông tại C ta có:

ND² = NC² + CD² = NC² + (2NC)² = 5NC².

Do đó, $\frac{N{C}^2}{N{D}^2}=\frac{1}{5}$  . Suy ra $\frac{NC}{ND}=\frac{1}{\sqrt{5}}$ .

Xét tam giác NOC vuông tại O và tam giác CND vuông tại C có:

$\widehat{ONC}$ chung

Do đó, ∆ONC ᔕ ∆CND  (góc nhọn).

Suy ra $\frac{ON}{CN}=\frac{OC}{CD}=\frac{NC}{ND}=\frac{1}{\sqrt{5}}$ . Do đó, OC = $\frac{1}{\sqrt{5}}$ CD; ON = CN.

Vậy diện tích tam giác ONC là:

$S=\frac{1}{2}OC\cdot ON=\frac{1}{2}.\frac{1}{\sqrt{5}}CD\cdot \frac{1}{\sqrt{5}}CN=\frac{1}{10}\cdot 4\cdot 2=0,8$ (cm²).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: