Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH

Bài 9.46 trang 63 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Trả lời

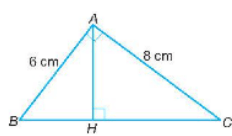
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 6² + 8² = 100

Nên BC = 10 cm.

Vì AH là đường cao trong tam giác ABC nên AH vuông góc với BC.

Tam giác ABC vuông tại A và tam giác HAC vuông tại H có:

$\widehat{C}$ chung

Do đó, ∆ABC ᔕ ∆HAC (góc nhọn).

Suy ra $\frac{AC}{HC}=\frac{BC}{AC}$  nên CH = $\frac{C{A}^2}{CB}=\frac{8^2}{10}=\frac{32}{5}=6,4$ (cm).

Do đó, BH = BC – CH = 10 – 6,4 = 3,6  (cm).

Vì ∆ABC ᔕ ∆HAC (cmt) nên $\frac{AB}{HA}=\frac{BC}{AC}$ .

Do đó, AH = $\frac{AB\cdot AC}{BC}=\frac{6\cdot 8}{10}=4,8$  (cm).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: