Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường
398
03/12/2023
Bài 8 trang 120 Toán 7 Tập 2: Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144).
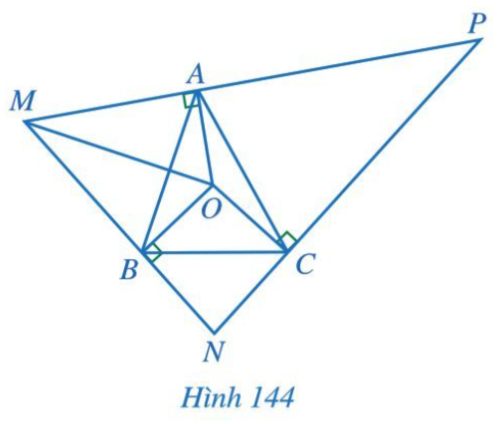
Chứng minh:
a) OMA = OMB và tia MO là tia phân giác của góc NMP;
b) O là giao điểm ba đường phân giác của tam giác MNP.
Trả lời
|
GT
|
ABC, O là giao điểm của ba đường trung trực,
MP OA, MN OB, NP OC
|
|
KL
|
a) OMA = OMB và tia MO là tia phân giác của
b) O là giao điểm ba đường phân giác của tam giác MNP.
|
Chứng minh (Hình 144):
a) Vì O là giao điểm ba đường trung trực của tam giác ABC nên OA = OB = OC.
Xét OAM (vuông tại A) và OBM (vuông tại B) có:
OM là cạnh chung,
OA = OB (chứng minh trên),
Do đó OAM = OBM (cạnh huyền - cạnh góc vuông).
Suy ra (hai góc tương ứng).
Khi đó MO là tia phân giác của hay MO là tia phân giác của .
Vậy tia MO là tia phân giác của
b) Nối OP (Hình vẽ dưới đây):
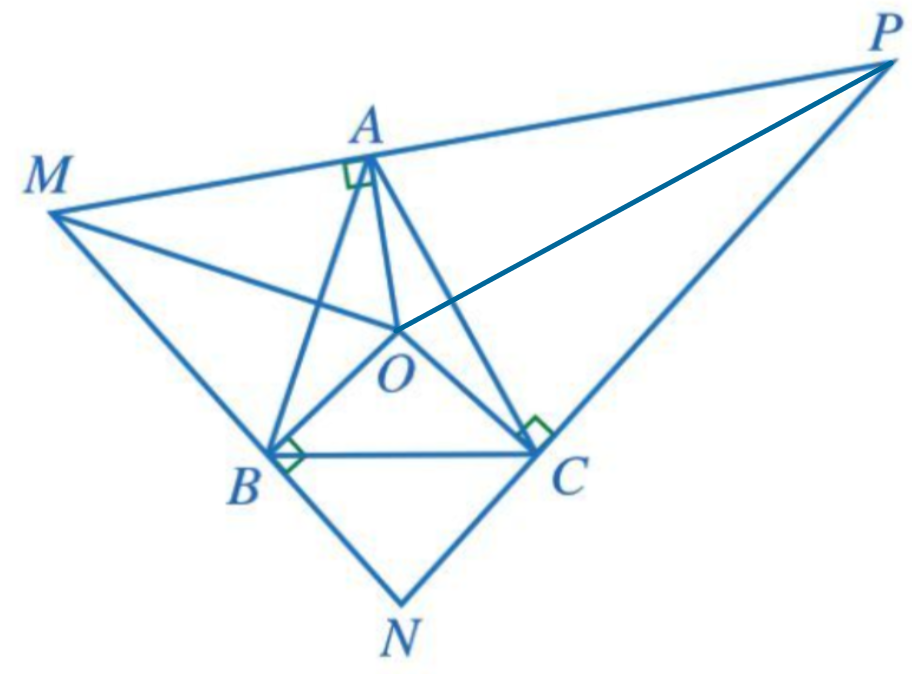
Xét OAP (vuông tại A) và OCP (vuông tại C) có:
OP là cạnh chung,
OA = OC (chứng minh trên),
Do đó OAP = OCP (cạnh huyền - cạnh góc vuông).
Suy ra (hai góc tương ứng).
Khi đó PO là tia phân giác của hay PO là tia phân giác của .
Trong một tam giác, ba đường phân giác của tam giác đó luôn cùng đi qua một điểm
Mà O là giao điểm hai đường phân giác của góc và góc, do đó O là giao điểm ba đường phân giác của tam giác MNP.
Vậy O là giao điểm ba đường phân giác của tam giác MNP.
Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 9: Đường trung trực của một đoạn thẳng
Bài 10: Tính chất ba đường trung tuyến của tam giác
Bài 11: Tính chất ba đường phân giác của tam giác
Bài 12: Tính chất ba đường trung trực của tam giác
Bài 13: Tính chất ba đường cao của tam giác
Bài tập cuối chương 7


