Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N. Chứng minh: a) Nếu OM = ON thì AM // BN

Bài 5 trang 119 Toán 7 Tập 2: Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N.

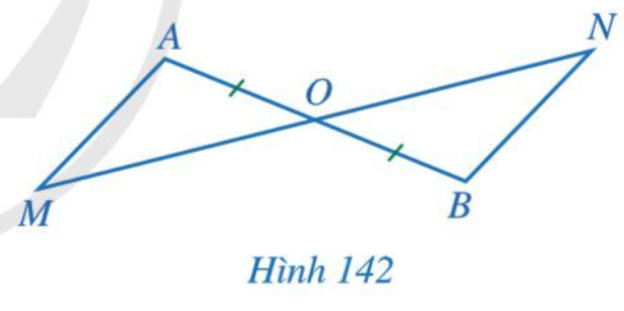
Chứng minh:

a) Nếu OM = ON thì AM // BN;

b) Nếu AM // BN thì OM = ON.

Trả lời

a)

Chứng minh (Hình 142):

Xét $∆$OAM và $∆$OBN có:

AO = BO (do M là trung điểm của AB),

$\widehat{AOM}=\widehat{BON}$ (hai góc đối đỉnh),

OM = ON (giả thiết).

Do đó $∆$OAM = $∆$OBN (c.g.c).

Suy ra $\widehat{AM\text{O}}=\widehat{BNO}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong nên AM // BN (dấu hiệu nhận biết)

Vậy AM //BN.

b)

Chứng minh (Hình 142):

Do AM // BN (giả thiết) nên $\widehat{MAO}=\widehat{NBO}$ (hai góc so le trong).

Xét $∆$OAM và $∆$OBN có:

$\widehat{MAO}=\widehat{NBO}$ (chứng minh trên),

AO = BO (do M là trung điểm của AB),

$\widehat{AOM}=\widehat{BON}$ (hai góc đối đỉnh).

Do đó $∆$OAM = $∆$OBN (g.c.g).

Suy ra OM = ON (hai cạnh tương ứng).

Vậy OM = ON.

Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 9: Đường trung trực của một đoạn thẳng

Bài 10: Tính chất ba đường trung tuyến của tam giác

Bài 11: Tính chất ba đường phân giác của tam giác

Bài 12: Tính chất ba đường trung trực của tam giác

Bài 13: Tính chất ba đường cao của tam giác

Bài tập cuối chương 7