Giải SGK Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác

Q: Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó

Vậy AD là đường trung tuyến của tam giác ABC.

Tổng quan

Hỏi đáp (10)

Chủ đề (4)

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 7 Bài 11: Tính chất ba đường phân giác của tam giác sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 11. Mời các bạn đón xem:

Giải SGK Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác

A. Câu hỏi trong bài

Giải Toán 7 trang 108 Tập 2

Câu hỏi khởi động trang 108 Toán 7 Tập 2:

Bạn Ngân gấp một miếng bìa hình tam giác để các nếp gấp tạo thành ba tia phân giác của các góc ở đỉnh của tam giác đó (Hình 109).

Ba nếp gấp đó có đặc điểm gì?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Ba nếp gấp đó lần lượt là ba đường phân giác của ba góc trong tam giác và ba nếp gấp này cùng đi qua một điểm.

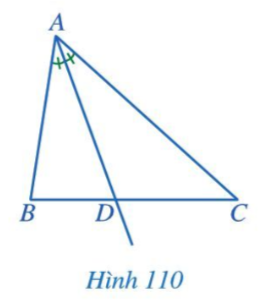
Hoạt động 1 trang 108 Toán 7 Tập 2:

Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì?

Lời giải:

Hai đầu mút của đoạn thẳng AD có đặc điểm:

+ A là đỉnh của tam giác ABC;

+ D là giao điểm của đường phân giác của góc A và cạnh BC.

Giải Toán 7 trang 109 Tập 2

Luyện tập 1 trang 109 Toán 7 Tập 2: Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.

Lời giải:

$∆$ ABC cân tại A,

AD là đường phân giác của $\hat{B A C},$

AD là đường trung tuyến của tam giác ABC.

Chứng minh (Hình vẽ dưới đây):

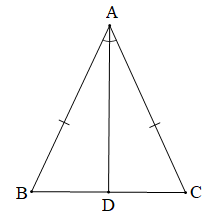
Giải Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác (ảnh 1)

Vì tam giác ABC cân tại A (giả thiết) nên AB = AC.

Vì AD là đường phân giác của $\hat{B A C}$ (giả thiết) nên $\hat{B A D} = \hat{C A D}$ .

Xét $∆$ ABD và $∆$ ACD có:

AB = AC (chứng minh trên),

$\hat{B A D} = \hat{C A D}$ (chứng minh trên),

AD chung

Do đó $Δ A B D = Δ A C D$ (c.g.c).

Suy ra BD = CD (hai cạnh tương ứng).

Mà D nằm giữa B và C nên D là trung điểm của BC

Do đó AD là đường trung tuyến kẻ từ đỉnh A của $∆$ ABC.

Vậy AD là đường trung tuyến của $∆$ ABC.

Hoạt động 2 trang 109 Toán 7 Tập 2: Quan sát các đường phân giác AD, BE, CK của tam giác ABC (Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không.

Lời giải:

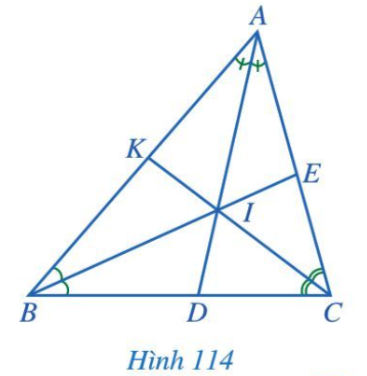
Quan sát Hình 144 ta thấy ba đường phân giác AD, BE, CK của tam giác ABC cùng đi qua điểm I.

Giải Toán 7 trang 110 Tập 2

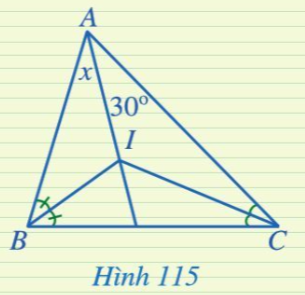
Luyện tập 2 trang 110 Toán 7 Tập 2: Tìm số đo x trong Hình 115.

Lời giải:

Vì đường phân giác của góc B và góc C cắt nhau tại I nên I là giao điểm ba đường phân giác của tam giác ABC.

Do đó AI là đường phân giác của $\hat{B A C}$ .

Suy ra $\hat{B A I} = \hat{I A C} = 30 °$ (tính chất tia phân giác của một góc)

Nên x = 30°.

Vậy x = 30°.

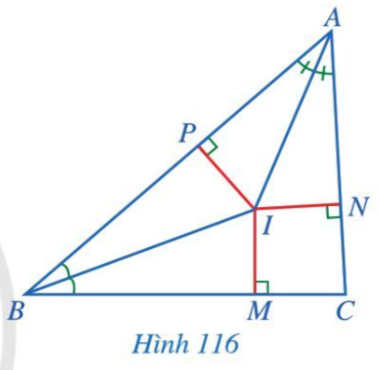
Hoạt động 3 trang 110 Toán 7 Tập 2:

Quan sát giao điểm I của ba đường phân giác trong tam giác ABC (Hình 116) và so sánh độ dài ba đoạn thẳng IM, IN, IP.

Lời giải:

Xét $∆$ AIP (vuông tại P) và $∆$ AIN (vuông tại N) có:

$\hat{P A I} = \hat{N A I}$ (AI là tia phân giác của $\hat{B A C}$ ),

AI là cạnh chung,

Do đó $∆$ AIP = $∆$ AIN (cạnh huyền - góc nhọn).

Suy ra IP = IN (hai cạnh tương ứng) (1)

Xét $∆$ BIP (vuông tại P) và $∆$ BIM (vuông tại M) có:

$\hat{P B I} = \hat{M B I}$ (BI là tia phân giác của $\hat{A B C}$ ),

BI là cạnh chung,

Do đó $∆$ BIP = $∆$ BIM (cạnh huyền - góc nhọn).

Suy ra IP = IM (hai cạnh tương ứng) (2)

Từ (1) và (2) suy ra IP = IM = IN.

Vậy IP = IM = IN.

Giải Toán 7 trang 111 Tập 2

Luyện tập 3 trang 111 Toán 7 Tập 2:

Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.

Lời giải:

$∆$ ABC, I là giao điểm của ba đường phân giác,

M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB

IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.

Chứng minh (Hình vẽ dưới đây):

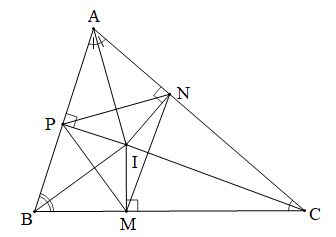
Giải Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác (ảnh 1)

Do M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (giả thiết)

Nên IM $⊥$ BC, IN $⊥$ AC, IP $⊥$ AB.

Vì I là giao điểm của ba đường phân giác (giả thiết)

Nên IM = IN = IP (tính chất giao điểm ba đường phân giác)

+) Chứng minh IA là đường trung trực của đoạn thẳng NP.

Vì IN = IP (chứng minh trên) nên I thuộc đường trung trực của NP (1)

Xét $∆$ API (vuông tại P) và $∆$ ANI (vuông tại N) có:

AI là cạnh chung,

IP = IN (chứng minh trên)

Do đó $∆$ API = $∆$ ANI (cạnh huyền - cạnh góc vuông).

Suy ra AP = AN (hai cạnh tương ứng).

Do đó A thuộc đường trung trực của NP (2)

Từ (1) và (2) suy ra IA là đường trung trực của NP.

+) Chứng minh IB là đường trung trực của PM.

Vì IP = IM (chứng minh trên) nên I thuộc đường trung trực của PM. (3)

Xét $∆$ BMI (vuông tại M) và $∆$ BPI (vuông tại P) có:

BI là cạnh chung,

IM = IP (chứng minh trên)

Do đó $∆$ BMI = $∆$ BPI (cạnh huyền - cạnh góc vuông).

Suy ra BM = BP (hai cạnh tương ứng).

Do đó B thuộc đường trung trực của PM. (4)

Từ (3) và (4) suy ra IB là đường trung trực của PM.

+) Chứng minh IC là đường trung trực của MN.

Vì IM = IN (chứng minh trên) nên I thuộc đường trung trực của MN. (5)

Xét $∆$ CMI (vuông tại M) và $∆$ CNI (vuông tại N) có:

CI là cạnh chung,

IM = IN (chứng minh trên).

Do đó $∆$ CMI = $∆$ CNI (cạnh huyền - cạnh góc vuông).

Suy ra CM = CN (hai cạnh tương ứng).

Do đó C thuộc đường trung trực của MN. (6)

Từ (5) và (6) suy ra IC là đường trung trực của MN.

B. Bài tập

Bài 1 trang 111 Toán 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.

a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?

b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?

Lời giải:

$∆$ ABC, I là giao điểm của ba đường phân giác,

M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB

a) $∆$ IMN, $∆$ INP, $∆$ IPM có là tam giác cân không? Vì sao?

b) $∆$ ANP, $∆$ BPM, $∆$ CMN có là tam giác cân không? Vì sao?

Chứng minh (Hình vẽ dưới đây):

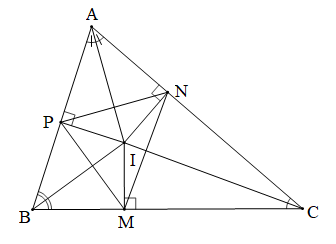
Giải Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác (ảnh 1)

a) Do M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (giả thiết)

Nên IM $⊥$ BC, IN $⊥$ AC, IP $⊥$ AB.

Vì I là giao điểm của ba đường phân giác (giả thiết)

Nên IM = IN = IP (tính chất giao điểm ba đường phân giác)

Vì IM = IN nên $∆$ IMN cân tại I.

Vì IN = IP nên $∆$ INP cân tại I.

Vì IP = IM nên $∆$ IPM cân tại I.

b) +) Xét $∆$ API (vuông tại P) và $∆$ ANI (vuông tại N) có:

AI là cạnh chung,

IP = IN (chứng minh trên)

Do đó $∆$ API = $∆$ ANI (cạnh huyền - cạnh góc vuông).

Suy ra AP = AN (hai cạnh tương ứng).

Tam giác ANP có AP = AN nên tam giác ANP cân tại A.

+) Xét $∆$ BMI (vuông tại M) và $∆$ BPI (vuông tại P) có:

BI là cạnh chung,

IM = IP (chứng minh trên)

Do đó $∆$ BMI = $∆$ BPI (cạnh huyền - cạnh góc vuông).

Suy ra BM = BP (hai cạnh tương ứng).

Tam giác BPM có BP = BM nên tam giác BPM cân tại B.

+) Xét $∆$ CMI (vuông tại M) và $∆$ CNI (vuông tại N) có:

CI là cạnh chung,

IM = IN (chứng minh trên).

Do đó $∆$ CMI = $∆$ CNI (cạnh huyền - cạnh góc vuông).

Suy ra CM = CN (hai cạnh tương ứng).

Tam giác CMN có CM = CN nên tam giác CMN cân tại C.

Bài 2 trang 111 Toán 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:

a) $\hat{I A B} + \hat{I B C} + \hat{I C A} = 90 °$ ;

b) $\hat{B I C} = 90 ° + \frac{1}{2} \hat{B A C}$ .

Lời giải:

$∆$ ABC, I là giao điểm của ba đường phân giác

a) $\hat{I A B} + \hat{I B C} + \hat{I C A} = 90 °$ ;

b) $\hat{B I C} = 90 ° + \frac{1}{2} \hat{B A C}$ .

Chứng minh (Hình vẽ dưới đây):

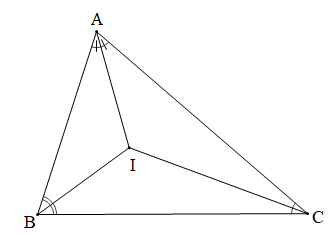
Giải Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác (ảnh 1)

a) Vì AI là đường phân giác của $\hat{B A C}$ nên $\hat{I A B} = \frac{1}{2} \hat{B A C}$ (tính chất tia phân giác của một góc)

Vì BI là đường phân giác của $\hat{A B C}$ nên $\hat{I B C} = \frac{1}{2} \hat{A B C}$ (tính chất tia phân giác của một góc)

Vì CI là đường phân giác của $\hat{A C B}$ nên $\hat{I C A} = \frac{1}{2} \hat{A C B}$ (tính chất tia phân giác của một góc)

Suy ra $\hat{I A B} + \hat{I B C} + \hat{I C A} = \frac{1}{2} \hat{B A C} + \frac{1}{2} \hat{A B C} + \frac{1}{2} \hat{A C B} = \frac{1}{2} (\hat{B A C} + \hat{A B C} + \hat{A C B})$

Xét tam giác ABC ta có $\hat{B A C} + \hat{A B C} + \hat{A C B} = 180 °$ (tổng ba góc của một tam giác)

Do đó $\hat{I A B} + \hat{I B C} + \hat{I C A} = \frac{1}{2} .180 ° = 90 °$ .

Vậy $\hat{I A B} + \hat{I B C} + \hat{I C A} = 90 ° .$

b) Vì CI là đường phân giác của $\hat{A C B}$ nên $\hat{I C A} = \hat{I C B} = \frac{1}{2} \hat{A C B}$ .

Suy ra $\hat{I A B} + \hat{I B C} + \hat{I C B} = 90 °$ .

Do đó $\hat{I B C} + \hat{I C B} = 90 ° - \hat{I A B} = 90 ° - \frac{1}{2} \hat{B A C}$ .

Xét tam giác BIC có: $\hat{B I C} + \hat{I B C} + \hat{I C B} = 180 °$ (tổng ba góc của một tam giác)

Do đó $\hat{B I C} = 180 ° - (\hat{I B C} + \hat{I C B}) = 180 ° - (90 ° - \frac{1}{2} \hat{B A C}) = 90 ° + \frac{1}{2} \hat{B A C}$ .

Vậy $\hat{B I C} = 90 ° + \frac{1}{2} \hat{B A C} .$

Bài 3 trang 111 Toán 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.

a) Chứng minh $\hat{C B I} > \hat{A C I}$ ;

b) So sánh IB và IC.

Lời giải:

$∆$ ABC, AB < AC,

I là giao điểm của ba đường phân giác

a) $\hat{C B I} > \hat{A C I}$

b) So sánh IB và IC.

Chứng minh (Hình vẽ dưới đây):

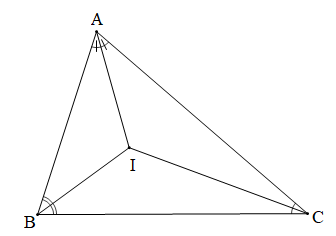
Giải Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác (ảnh 1)

a) Vì BI là đường phân giác của $\hat{A B C}$ nên $\hat{A B I} = \hat{C B I} = \frac{1}{2} \hat{A B C}$ .

Vì CI là đường phân giác của $\hat{A C B}$ nên $\hat{A C I} = \hat{B C I} = \frac{1}{2} \hat{A C B}$ .

Tam giác ABC có AB < AC nên $\hat{A C B} < \hat{A B C}$ (quan hệ giữa góc và cạnh đối diện trong một tam giác)

Do đó $\frac{1}{2} \hat{A C B} < \frac{1}{2} \hat{A B C}$ .

Suy ra $\hat{A C I} < \hat{C B I}$ .

Vậy $\hat{C B I} > \hat{A C I} .$

b) Vì $\hat{A C I} < \hat{C B I}$ (chứng minh câu a), mà $\hat{A C I} = \hat{B C I}$ nên $\hat{B C I} < \hat{C B I}$ .

Tam giác BIC có $\hat{B C I} < \hat{C B I}$ nên IB < IC (quan hệ giữa cạnh và góc đối diện trong một tam giác)

Vậy IB < IC.

Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 9: Đường trung trực của một đoạn thẳng

Bài 10: Tính chất ba đường trung tuyến của tam giác

Bài 12: Tính chất ba đường trung trực của tam giác

Bài 13: Tính chất ba đường cao của tam giác

Bài tập cuối chương 7

Câu hỏi liên quan

Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó

Vậy AD là đường trung tuyến của tam giác ABC.
Xem thêm

Tìm số đo x trong Hình 115

Vậy x = 30°.
Xem thêm

Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC. Chứng minh góc CBI > góc ACI

Vậy IB < IC.
Xem thêm

Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB

Từ (5) và (6) suy ra IC là đường trung trực của MN.
Xem thêm

Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh: góc IAB + góc IBC + góc ICA = 90°

Vậy góc BIC = 90 độ + 1/2 góc BAC.
Xem thêm

Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB

Tam giác CMN có CM = CN nên tam giác CMN cân tại C.
Xem thêm

Quan sát các đường phân giác AD, BE, CK của tam giác ABC (Hình 114), cho biết ba đường phân giác đó có cùng đi qua một điểm hay không

Quan sát Hình 144 ta thấy ba đường phân giác AD, BE, CK của tam giác ABC cùng đi qua điểm I.
Xem thêm

Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại điểm D (Hình 110). Các đầu mút của đoạn thẳng AD có đặc điểm gì

+ D là giao điểm của đường phân giác của góc A và cạnh BC.
Xem thêm

Quan sát giao điểm I của ba đường phân giác trong tam giác ABC (Hình 116) và so sánh độ dài ba đoạn thẳng IM, IN, IP

Vậy IP = IM = IN.
Xem thêm

Bạn Ngân gấp một miếng bìa hình tam giác để các nếp gấp tạo thành ba tia phân giác của các góc ở đỉnh của tam giác đó (Hình 109)

Ba nếp gấp đó lần lượt là ba đường phân giác của ba góc trong tam giác và ba nếp gấp này cùng đi qua một điểm.
Xem thêm

Xem tất cả hỏi đáp với chuyên mục: Tính chất ba đường phân giác của tam giác

Được cập nhật 16/11/2023 343 lượt xem

Bởi Quynh Anh

Chủ đề: giải sgk Toán 7 Tính chất ba đường phân giác của tam giác

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Giải sgk Toán 7 - CD

Giải SGK Toán 7 Bài 1 (Cánh diều): Góc ở vị trí đặc biệt

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 7 Bài 1 (Cánh diều): Góc ở vị trí đặc biệt sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 1. Mời các bạn đón xem:

513 1 năm trước

Giải sgk Toán 7 - CD

Giải SGK Toán 7 Chủ đề 3 (Cánh diều): Dung tích phổi

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 7 Bài dung dịch điều phổi sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài dung dịch điều phổi. Mời các bạn đón xem:

426 1 năm trước

Giải sgk Toán 7 - CD

Giải SGK Toán 7 (Cánh diều): Bài tập cuối chương 7

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 7 Bài tập cuối chương 7 sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài tập cuối chương 7. Mời các bạn đón xem:

328 1 năm trước