Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a căn bậc hai 3. Gọi M, N lần lượt là trung điểm của SB, SC. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC).
55
21/05/2024
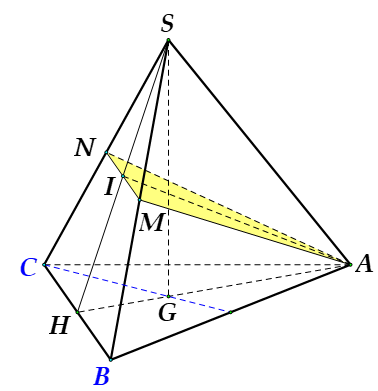
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a√3. Gọi M, N lần lượt là trung điểm của SB, SC. Biết mặt phẳng (AMN) vuông góc với mặt phẳng (SBC). Tính thể tích của khối chóp A.BCNM .
A. 3a3√1516
B. 3a3√1548
C. 3a3√1532
D. a3√1532
Trả lời
Chọn C
Gọi H là trung điểm BC⇒BC⊥SH (do ΔSBC cân tại I ).
Gọi G là trọng tâm ΔABC và I=SH∩MN.
Do S.ABC là chóp đều ⇒SG⊥(ABC)
Ta có: MN là đường trung bình của ΔSBC⇒MN//BC⇒MN⊥SH tại I
Vậy: {(AMN)⊥(SBC)(AMN)∩(SBC)=MNSH⊥MN,SH⊂(SBC)⇒SH⊥(AMN)⇒SH⊥AI
Lại có I là trung điểm SH (do I∈MN) => AI là đường trung tuyến ΔSAH
Suy ra ΔSAH cân tại A⇒SA=AH=AB√32=3a2
Xét ΔSGA vuông tại G : SG=√SA2−AG2=√(3a2)2−(23.3a2)2=a√52
Mặt khác: VS.AMNVS.ABC=SMSB.SNSC=14⇒VMNABC=34VS.ABC=34.13.SG.AB2√34=3√1532a3