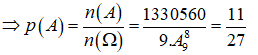299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P8)
-
735 lượt thi
-
40 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xếp 4 người đàn ông, 2 người đàn bà và một đứa trẻ được xếp ngồi vào 7 chiếc ghế đặt quanh một bàn tròn. Xác suất để xếp đứa trẻ ngồi giữa hai người đàn ông là
 Xem đáp án
Xem đáp án
Chọn D
Gọi A là biến cố “ Xếp 7 người sao cho đứa trẻ ngồi giữa hai người đàn ông”
Ta có: ![]()
Xếp thỏa mãn đề bài theo các bước sau:
+Cố định đứa trẻ vào 1 ghế.
+Vì đứa trẻ ngồi giữa 2 người đàn ông nên xếp 2 người đàn ông ngồi bên cạnh đứa trẻ
có: (cách)
+Xếp 2 người đàn ông còn lại và 2 người đàn bà vào 4 ghế còn lại có: 4! (cách)
![]()
Vậy 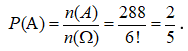
Câu 2:
Gọi S là tập hợp các số tự nhiên gồm 9 chữ số được lập từ X = {6;7;8}, trong đó chữ số 6 xuất hiện 2 lần; chữ số 7 xuất hiện 3 lần; chữ số 8 xuất hiện 4 lần. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6 là
 Xem đáp án
Xem đáp án
Chọn A
Cách 1:
Ta có S là tập hợp các số tự nhiên gồm 9 chữ số được lập từ X = {6;7;8}, trong đó chữ số 6 xuất hiện 2 lần; chữ số 7 xuất hiện 3 lần; chữ số 8 xuất hiện 4 lần nên
Có cách xếp 2 chữ số 6 vào 2 trong 9 vị trí
Có cách xếp 3 chữ số 7 vào 3 trong 7 vị trí còn lại
Có 1 cách xếp 4 chữ số 8 vào 4 trong 4 vị trí còn lại
![]()
Chọn ngẫu nhiên một số từ tập S nên ![]()
Gọi A là biến cố “số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6”
TH1: 2 chữ số 6 đứng liền nhau
Có 8 cách xếp cho số .Trong mỗi cách như vậy có cách xếp chữ số 7 và 1 cách xếp cho các chữ số 8
Vậy có số 8..1 = 280 số
TH2: Giữa hai số 6 có đúng 1 chữ số và số đó là số 8.
Có 7 cách xếp cho số .Trong mỗi cách như vậy có cách xếp chữ số 7 và 1 cách xếp các chữ số 8
Vậy có 7. = 140 số
TH3: Giữa hai số 6 có đúng 2 chữ số và đó là hai chữ số 8.
Tương tự Có 6. = 60 số
TH4: Giữa hai số 6 có đúng 3 chữ số và đó là ba chữ số 8.
Có 5. = 20 số
TH5: Giữa hai số 6 có đúng 4 chữ số và đó là bốn chữ số 8.
Có 4. = 4 số
Từ đó suy ra ![]()
Xác suất cần tìm là ![]()
Cách 2:
- Số phần tử không gian mẫu ![]()
- Tính số phần tử của biến cố A“số được chọn là số không có chữ số 7 đứng giữa hai chữ số 6”
Xếp 2 số 6 có 1 cách: ![]()
Xếp 3 số 7 vào 2 khoảng ![]() cách ( số cách xếp bằng số nghiệm nguyên không âm của phương trình
cách ( số cách xếp bằng số nghiệm nguyên không âm của phương trình ![]()
![]()
Xác suất cần tìm là ![]()
Câu 3:
Cho một bảng ô vuông 3x3

Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng:
 Xem đáp án
Xem đáp án
Chọn B
Ta có ![]()
Xét : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó ![]()
Vậy ![]()
Câu 4:
Trong kỳ thi Chọn học sinh giỏi tỉnh có em dự thi, có 105 em tham gia buổi gặp mặt trước kỳ thi. Biết các em đó có số thứ tự trong danh sách lập thành một cấp số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ ngồi được 1 học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau.
 Xem đáp án
Xem đáp án
Chọn B.
Giả sử số thứ tự trong danh sách là ![]()
Do dãy này là cấp số cộng nên ta có ![]()
![]()
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự cặp học sinh có các cặp số thứ tự là ![]()
![]()
vào trước cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước . Bước này có cách.
Suy ra số kết quả thuận lợi cho biến cố A là ![]()
Vậy xác suất của biến cố A là ![]()
Câu 5:
Trong mặt phẳng, cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm và trên tia Oy lấy 10 điểm thỏa mãn (đvd). Chọn ra ngẫu nhiên một tam giác có đỉnh nằm trong 20 điểm . Xác suất để tam giác chọn được có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy là
 Xem đáp án
Xem đáp án
Chọn B
· Bổ đề: Trong mặt phẳng cho hai tia Ox và Oy vuông góc với nhau tại gốc O. Trên tia Ox lấy 10 điểm và trên tia Oy lấy 10 điểm thỏa mãn (đvd).
Tìm số tam giác có 2 đỉnh nằm trong 10 điểm ![]() 1 đỉnh nằm trong 10 điểm sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
1 đỉnh nằm trong 10 điểm sao cho tam giác chọn được có đường tròn ngoại tiếp, tiếp xúc với một trong hai trục Ox hoặc Oy?
Giải: Gọi ![]() là 3 đỉnh của tam giác thỏa yêu cầu bài toán với
là 3 đỉnh của tam giác thỏa yêu cầu bài toán với ![]()
Ta có ![]()
Do đường tròn luôn cắt Ox tại ![]() phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại ta có phương tích
phân biệt nên đường tròn chỉ có thể tiếp xúc với Oy tại ta có phương tích
![]()
Do ![]() nên dễ thấy
nên dễ thấy ![]()
hay nói cách khác bộ ba (m,n,p) ![]()
Vậy có 4 tam giác thỏa mãn yêu cầu bổ đề.
· Bài toán: Không gian mẫu ![]()
Gọi A là biến cố chọn được tam giác có đường tròn ngoại tiếp tiếp xúc với một trong hai trục Ox hoặc Oy. Theo bổ đề ta chọn được 4 tam giác có 2 đỉnh thuộc tia Ox, 1 đỉnh thuộc tia Oy; tương tự có 4 tam giác có 1 đỉnh thuộc tia Oy, đỉnh thuộc tia . Suy ra, n(A) = 8
Xác suất biến cố A là 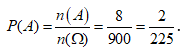
Câu 6:
Cho tập A = {0;1;2;3;4;5;6}. Xác suất để lập được số tự nhiên gồm 5 chữ số khác nhau lấy từ các phần tử của tập A sao cho số đó chia hết cho 1,2,3 và các chữ số 1,2,3 luôn có mặt cạnh nhau là
 Xem đáp án
Xem đáp án
Chọn D
Gọi số tự nhiên có chữ số khác nhau lấy từ các phần tử của tập A là ![]()
![]()
+) Chọn a có 6 cách.
+) Chọn bốn chữ số b,c,d,e có cách.
Vậy số cách lập số tự nhiên có 5 chữ số khác nhau lấy từ các phần tử của tập A là
6. = 2160 cách. Do đó số phần tử của không gian mẫu là ![]()
Gọi biến cố B: ‘‘Số tự nhiên lập được chia hết cho 5 và các chữ số 1,2,3 luôn có mặt cạnh nhau’’.
TH1: Số lập được có dạng
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có cách.
+) Chọn 1 số trong tập ![]()
+) Xếp khối X và số vừa chọn vào vị trí có cách.
Theo quy tắc nhân ta có .3 = 36 số.
TH2: Số lập được có dạng
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta có cách chọn số a,b,c
Vậy có = 6 số.
TH3: Số lập được có dạng ![]()
+) Vì các chữ số 1,2,3 luôn có mặt cạnh nhau nên ta coi ba số đó là khối X. Xếp ba số 1,2,3 trong khối X có cách.
+) Chọn số trong tập {4;6} có = 2 cách.
+) Xếp khối X và số vừa chọn vào vị trí có cách.
Theo quy tắc nhân ta có .2 = 24 số.
Vậy số kết quả xảy ra của biến cố B là ![]()
Xác suất của biến cố B là 
Câu 7:
Cho tập S = {1;2;3;...;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là
 Xem đáp án
Xem đáp án
Chọn C
Lấy 3 phần tử từ tập S có ![]()
Suy ra số phần tử của không gian mẫu là ![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán.
Đặt ![]() có 10 phần tử.
có 10 phần tử.
![]() có 10 phần tử.
có 10 phần tử.
a, b, c là ba số theo thứ tự lập thành cấp số cộng => 2a = b + c
Có 2a là số chẵn, nên b và c cùng chẵn hoặc cùng lẻ.
Suy ra số cách chọn b, c là ![]()
Mỗi cách chọn cặp b, c thì có duy nhất một cách chọn a sao cho 2a = b + c
Suy ra số phần tử của biến cố là ![]()
Xác suất thỏa yêu cầu bài là 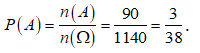

Câu 8:
Từ tập hợp tất cả các số tự nhiên có năm chữ số mà các chữ số đều khác 0, lấy ngẫu nhiên một số. Xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là:
 Xem đáp án
Xem đáp án
Chọn D
Không gian mẫu được mô tả là : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: 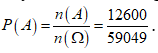
Câu 9:
Có 3 quả cầu màu vàng, 3 quả cầu màu xanh (các quả cầu cùng màu thì giống nhau) bỏ vào hai cái hộp khác nhau, mỗi hộp quả cầu. Tính xác suất để các quả cầu cùng màu thì vào chung một hộp.
 Xem đáp án
Xem đáp án
Chọn A
* Không gian mẫu là = 6
* Gọi biến cố A: " Các quả cầu cùng màu thì vào chung một hộp”
Bỏ 3 quả cầu vào một hộp, bỏ 3 quả màu xanh vào hộp còn lại có 2 cách
=> n(A) = 2
* Xác suất của biến cố A là
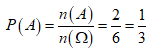
Câu 10:
Có 15 cuốn sách gồm 4 cuốn sách Toán, 5 cuốn sách Lý và 6 cuốn sách Hóa. Các cuốn sách đôi một khác nhau. Thầy giáo chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy còn đủ 3 môn
 Xem đáp án
Xem đáp án
Chọn C
Xét phép thử T: “Chọn 7 cuốn sách từ 15 cuốn sách”.
Số phần tử của không gian mẫu trong phép thử là .
Gọi A biến cố chọn 7 cuốn sách có đủ 3 môn trong phép thử T.
Xác suất của biến cố cần tìm bằng xác suất của biến cố A.
Ta có ![]()
Vậy
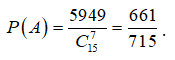
Câu 11:
Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng , trong đó 1abcd9
 Xem đáp án
Xem đáp án
Chọn D
Chọn số tự nhiên có 4 chữ số bất kỳ có: ![]() (cách).
(cách).
Gọi A là biến cố: “Số được chọn có dạng , trong đó 1abcd9” . (*)
Cách 1: Dùng tổ hợp
Nhận xét rằng với 2 số tự nhiên bất kỳ ta có: ![]()
Do đó nếu đặt:

Từ giả thuyết ![]() ta suy ra:
ta suy ra: ![]()
Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ {1,2,....,12}ta đều có được duy nhất một bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số (a,b,c,d) thoả mãn (*). Số cách chọn tập con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó:
![]()
Vậy 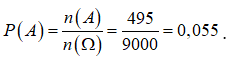
Cách 2: Dùng tổ hợp lặp
Chọn số tự nhiên có 4 chữ số bất kỳ có: ![]() (cách).
(cách).
Mỗi tập con có 4 phần tử được lấy từ tập {1,2,...,9}(trong đó mỗi phần tử có thể được chọn lặp lại nhiều lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được một số tự nhiên có dạng (trong đó ![]() ). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử
). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử
Do đó theo công thức tổ hợp lặp ta có: ![]()
Vậy 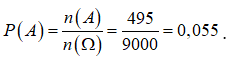
Câu 12:
Xếp ngẫu nhiên 2 quả cầu xanh, 2 quả cầu đỏ, 2 quả cầu trắng (các quả cầu này đôi một khác nhau) thành một hàng ngang. Tính xác suất để 2 quả cầu màu trắng không xếp cạnh nhau?
 Xem đáp án
Xem đáp án
Chọn A
Xếp ngẫu nhiên 6 quả cầu đôi một khác nhau thành một hàng ngang có 6! cách xếp.
Gọi A là biến cố “2 quả cầu màu trắng không xếp cạnh nhau”.
Suy ra là biến cố “2 quả cầu màu trắng xếp cạnh nhau”.
Ta có n() = 2.5!. Vậy xác suất cần tìm là ![]()
Câu 13:
Lập một số tự nhiên có 4 chữ số. Tính xác suất để số đó có chữ số đứng trước không nhỏ hơn chữ số đứng sau.
 Xem đáp án
Xem đáp án
Chọn C
Ta có 9.số tự nhiên có 4 chữ số.
Gọi số cần tìm có dạng ![]()
Cách 1: Ta có các trường hợp sau
* A > B > C > D: có ![]()
* A = B > C > D hoặc A > B = C > D hoặc A > B > C = D: ![]()
* A = B = C > D hoặc A = B > C = D hoặc A > B = C = D: ![]()
* A = B = C = D: có 9 số.
Vậy xác suất cần tìm là 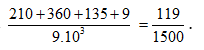
Cách 2:
Ta có ![]()
![]()
Do đó có cách chọn bộ 4 số D, C + 1, B + 2, A + 3
Suy ra, có cách chọn bộ số D, C, B, A
Trong số cách chọn đó, bỏ đi bộ số 0, 1, 2, 3
Vậy xác suất cần tìm là 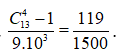
Câu 14:
Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm ở hai bảng khác nhau bằng
 Xem đáp án
Xem đáp án
Chọn D
Nhận định bài toán:
1) Đây là dạng bài toán phân chia một tập hợp ra thành các nhóm có số lượng bằng nhau.
2) Phương pháp:
Dạng bài toán này được phân chia làm 2 loại đó là:
- Các nhóm có thứ tự A, B, C, D…
- Các nhóm không phân biệt thứ tự.
Nếu không phân biệt rõ ràng 2 bài toán này thì rất dễ dẫn đến nhầm lẫn và sai kết quả.
Ví dụ: Có bao nhiêu cách chia 20 người thành 4 nhóm, mỗi nhóm có 5 người trong các trường hợp sau:
a) Các nhóm được đánh tên theo thứ tự A, B, C, D.
b) Không phân biệt thứ tự nhóm.
Lời giải
a) Số cách chọn 5 người cho nhóm A là . Ứng với mỗi cách chọn trên, ta có số cách chọn 5 người cho nhóm B là , nhóm C là và 5 người còn lại vào nhóm D.
Theo quy tắc nhân, ta được số cách chia nhóm là: 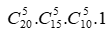 (cách).
(cách).
b) Vì các nhóm không phân biệt thứ tự nên khi ta hoán vị 4 nhóm trên sẽ cho cùng một kết quả. Do đó số cách chia trong trường hợp này là
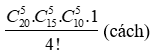
3) Phân tích bài toán và lời giải.
Chia 8 đội thành hai bảng đấu, do đó hai bảng đấu này sẽ có thứ tự rõ ràng cho nên bài toán của chúng ta thuộc loại chia nhóm có thứ tự.
Gọi hai bảng đấu là bảng A và bảng B.
Chọn 4 đội vào bảng A ta có cách, bốn đội còn lại vào bảng B có 1 cách.
Theo quy tắc nhân, ta có số cách chia 8 đội vào hai bảng đấu là:
![]()
Gọi A là biến cố “Hai đội Việt Nam nằm ở hai bảng khác nhau”.
Bảng A: Có 3 đội nước ngoài và 1 đội Việt Nam. Số cách chọn là .
Bảng B: Chỉ còn 1 cách chọn duy nhất cho 3 đội nước ngoài và 1 đội Việt Nam còn lại vào bảng B.
Do đó số cách chia 8 đội thành 2 bảng mỗi bảng có 1 đội Việt Nam là : n(A) = .1 = 40 cách
Vậy xác suất của biến cố A là: 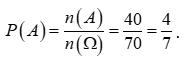
Câu 15:
Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của Việt Nam cùng nằm ở một bảng đấu.
 Xem đáp án
Xem đáp án
Chọn A
Gọi ba bảng đấu có tên là A, B, C.
Chọn 4 đội cho bảng A có cách, chọn 4 đội cho bảng B có cách và 4 đội còn lại vào bảng C có 1 cách.
Theo quy tắc nhân, số cách chia 12 đội thành 3 bảng đấu là: (cách)
Gọi A là biến cố “3 đội Việt Nam cùng nằm ở một bảng đấu.
Giả sử 3 đội Việt Nam cùng nằm ở bảng A.
Khi đó bảng A sẽ chọn 1 đội trong 9 đội nước ngoài và 3 đội Việt Nam, 8 đội còn lại chia vào bảng B và C. Trong trường hợp này ta có số cách chọn là ![]()
Vì vai trò của các bảng là như nhau nên trường hợp 3 đội Việt Nam ở bảng B hay bảng C đều cho kết quả như nhau.
Vậy số kết quả thuận lợi cho biến cố A là ![]()
Xác suất của biến cố A là : 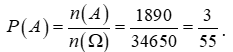
Câu 16:
Cho tập X = {1;2;3;....;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là
 Xem đáp án
Xem đáp án
Chọn C
+ Gọi số cần tìm là ![]()
Ta có tổng các chữ số của A là 1 + 2 + 3 + 4 + .... + 8 = 36 chia hết cho 9 nên A chia hết cho 9.
Do 9 và 111 có ƯCLN là nên A chia hết cho 9999.
Đặt ![]() Ta có:
Ta có:
![]() chia hết cho 9999 => x + y chia hết cho 9999
chia hết cho 9999 => x + y chia hết cho 9999
Mà ![]()
![]()
![]()
![]()
![]()
![]()
![]()
+ Từ tập X có 4 cặp số ![]() nên có: 8 cách chọn ; 6 cách chọn ; 4 cách chọn và 2 cách chọn .
nên có: 8 cách chọn ; 6 cách chọn ; 4 cách chọn và 2 cách chọn .
Vì và tạo thành một cặp để + = 9 nên chọn có luôn .
=> Số các số cần tìm là: 8.6.4.2 = 384 số
Vậy xác suất cần tìm là:
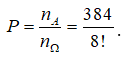
Câu 17:
Cho S là tập tất cả các số tự nhiên có 7 chữ số, lấy ngẫu nhiên một số từ tập S. Xác suất để số lấy được có chữ số tận cùng bằng 3 và chia hết cho 7 có kết quả gần nhất với số nào trong các số sau
 Xem đáp án
Xem đáp án
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó ![]()
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà ![]() nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
|
9999973 |
9999983 |
9999993 |
|
Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi A là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra ![]()
Câu 18:
Cho S là tập tất cả các số tự nhiên có 7 chữ số, lấy ngẫu nhiên một số từ tập S. Xác suất để số lấy được có chữ số tận cùng bằng 3 và chia hết cho 7 có kết quả gần nhất với số nào trong các số sau
 Xem đáp án
Xem đáp án
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó ![]()
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà ![]() nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
|
9999973 |
9999983 |
9999993 |
|
Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi A là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra ![]()
Câu 19:
Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm 2 chữ số phân biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng
 Xem đáp án
Xem đáp án
Chọn C
Cách 1: Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố thỏa mãn bài toán.
+ Khả năng 1: Hai bạn chọn số giống nhau nên có 81 cách.
+ Khả năng 2: Hai bạn chọn số đảo ngược của nhau nên có 9.8 = 72 cách.
+ Khả năng 3: Hai bạn chọn số chỉ có một chữ số trùng nhau
- TH1: Trùng chữ số 0: Công có 9 cách chọn số và Thành đều có 8 cách chọn số nên có 9.8 = 72 cách.
- TH 2: Trùng chữ số 1: Nếu Công chọn số 10 thì Thành có 16 cách chọn số có cùng chữ số 1. Nếu Công chọn số khác 10, khi đó Công có 16 cách chọn số và Thành có 15 cách chọn số có cùng chữ số 1 với Công nên có 16 + 16.15 = 16.16 256 cách.
- Các trường hợp chọn trùng chữ số 2,3,4,....,9 tương tự.
Vậy ![]()
Xác suất cần tính là 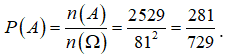
Cách 2: Số các số tự nhiên có hai chữ số phân biệt là 9.9= 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi là biến cố thỏa mãn bài toán. Xét biến cố
- TH 1: Công chọn số có dạng nên có 9 cách. Khi đó có 25 số có ít nhất một chữ số trùng với số nên Thành có 81 - 25 = 56 cách chọn số không có chữ số trùng với Công. Vậy có 9.56 = 504 cách.
- TH 2: Công chọn số không có dạng : Có 72 cách, khi đó 32 số có ít nhất một chữ số trùng với số của Công chọn nên Thành có 81 - 32 = 49 cách chọn số không có chữ số nào trùng với Thành. Vậy có 72.49 = 3528 cách.
![]()
![]()
Câu 20:
Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.
 Xem đáp án
Xem đáp án
Chọn A
Giả sử số cần lập là ![]()
Số phần từ không gian mẫu: ![]()
Gọi A là biến cố lấy được số chia hết cho 11 và tổng của các chữ số của chúng cũng chia hết cho 11.
Ta có:
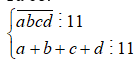
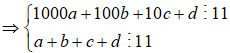
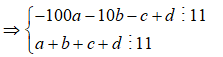
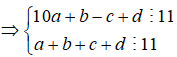
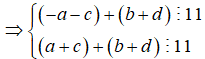
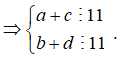
Từ 1,2,3,4,5,6,7,8,9 ta có 4 cặp tổng chia hết cho 11 là: ![]()
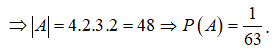
Câu 21:
Gọi A là tập các số tự nhiên có 3 chữ số đôi một khác nhau. Lấy ngẫu nhiên ra từ A hai số. Tính xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau.
 Xem đáp án
Xem đáp án
Chọn A
+ Số các chỉnh hợp chập của tập hợp các chữ số ![]()
Số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} mà chữ số 0 đứng vị trí đầu tiên () bằng số các chỉnh hợp chập của tập hợp các chữ số {0;1;2;3;4;5;6;7;8;9} và bằng .
Suy ra số các số tự nhiên có chữ số đôi một khác nhau bằng ![]()
+ Lấy ngẫu nhiên ra từ hai số có ![]() cách.
cách.
+ Gọi là biến cố “lấy được từ hai số mà các chữ số có mặt ở hai số đó giống nhau”
Trường hợp 1: Ba chữ số có mặt trong hai số được lấy không có chữ số 0
Chọn ba chữ số trong tập {0;1;2;3;4;5;6;7;8;9} có cách.
Ba chữ số này tạo thành 3! = 6 số trong A.
Lấy hai số trong 6 số này có cách (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có . cách lấy hai số thỏa trường hợp 1.
Trường hợp 2: Ba chữ số có mặt trong hai số được lấy có chữ số .
Chọn thêm hai chữ số trong tập {0;1;2;3;4;5;6;7;8;9}có cách.
Ba chữ số này (hai chữ số vừa chọn và chữ số 0) tạo thành 2.2! = 4 số trong A.
Lấy hai số trong 4 số này có (hai số các chữ số có mặt ở hai số đó giống nhau).
Suy ra có . cách lấy hai số thỏa trường hợp 2.
Suy ra ![]()
+ Do đó, xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau là:
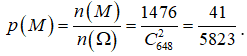
Câu 22:
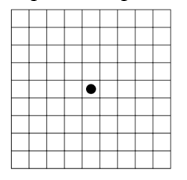
Cho một quân cờ đứng ở vị trí trung tâm của một bàn cờ 9x9 (xem hình vẽ). Biết rằng, mỗi lần di chuyển, quân cờ chỉ di chuyển sang ô có cùng một cạnh với ô đang đứng. Tính xác suất để sau bốn lần di chuyển, quân cờ không trở về đúng vị trí ban đầu.
 Xem đáp án
Xem đáp án
Chọn A
Mỗi lần di chuyển, quân cờ chỉ có thể di chuyển một trong bốn cách sau: lên trên 1 ô (U), xuống dưới 1 ô (D), sang phải 1 ô (R), sang trái 1 ô (L). Quân cờ di chuyển bốn lần sẽ có = 256 cách.
= 256 cách
Gọi A là biến cố quân cờ không trở về đúng vị trí ban đầu sau bốn lần di chuyển.
=> là biến cố quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển.
Để quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển thì phải thực hiện 1 trong 3 trường hợp sau:
Trường hợp 1: Có một U, một D, một R, một L.
Xếp cách thực hiện U, D, R, L theo thứ tự có 4! = 24 cách.
Trường hợp 2: Có hai U, hai D.
Xếp cách thực hiện hai U, hai D theo thứ tự có ![]() cách.
cách.
Trường hợp 3: Có hai R, hai L.
Xếp cách thực hiện hai R, hai L theo thứ tự có ![]() cách.
cách.

Câu 23:
Cho A là tập tất cả các số tự nhiên có 5 chữ số. Chọn ngẫu nhiên một số từ tập A, tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.
 Xem đáp án
Xem đáp án
Chọn A
Ta có tất cả các số tự nhiên có 5 chữ số bắt đầu từ 10000 đến 99999 gồm 90000 số.
Do đó = 90000
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 1.
Mà 90000 = 70x1285+50, nên ta chia 90000 số thành 1285 bộ 70 số liên tiếp và còn lại 50 số cuối, trong đó:
1285 bộ 70 số tự nhiên liên tiếp có 1285 số thỏa mãn yêu cầu
50 số cuối có 5 số tận cùng bằng 1 được xét trong bảng sau
|
99951 |
99961 |
99971 |
99981 |
99991 |
|
Chia cho 7 dư 5 |
Chia cho 7 dư 1 |
Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 3 |
Vậy tất cả có 1286 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.
Gọi là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1’ thì n(A) = 1286
Suy ra ![]()
Cách 2:
Vì A là tập tất cả các số tự nhiên có 5 chữ số nên
Số phần tử của không gian mẫu là ![]()
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
Khi ![]() có tận cùng bằng 1, do đó
có tận cùng bằng 1, do đó ![]() với
với ![]() có chữ số tận cùng là 3.
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng Khi đó: ![]()
- Với m = 1, do ![]()
+) Khi n = 4 thì p > 2 nên ![]() . Ta được 7 số thỏa mãn.
. Ta được 7 số thỏa mãn.
+) Khi n5 : Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p được chọn tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 50 số thỏa mãn.
- Với m2 tức là có 8 cách chọn m từ tập {2;3;4;5;6;7;8;9}. Khi đó ![]() với mọi n,p thuộc tập hợp {0;1;2;3;4;5;6;7;8;9}. Ta được 8.10.10 = 800 số thỏa mãn.
với mọi n,p thuộc tập hợp {0;1;2;3;4;5;6;7;8;9}. Ta được 8.10.10 = 800 số thỏa mãn.
2) M là số có 5 chữ số có dạng Khi đó: ![]()
Do 14285 nên m chỉ nhận giá trị bằng 1 và n 4
- Với m = 1; n = 0,1,2,3 thì p,q là các số tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 4.10.10 = 400 số thỏa mãn.
- Với m = 1; n = 4:
+) Khi p = 0 hoặc p = 1 thì q là số tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 2.10 = 20 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;1;2;3;4;5;6;7;8}. Ta được 9 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 7 + 50 + 8000 + 429 = 1286
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng

Câu 24:
Cho A là tập tất cả các số tự nhiên có 5 chữ số phân biệt. Chọn ngẫu nhiên một số từ tập tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1.
 Xem đáp án
Xem đáp án
Chọn A
Vì là tập tất cả các số tự nhiên có 5 chữ số nên
![]()
![]()
![]()
Số phần tử của không gian mẫu là ![]()
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
![]() có tận cùng bằng 1,do đó
có tận cùng bằng 1,do đó ![]() với
với ![]() có chữ số tận cùng là 3.
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng Khi đó: ![]()
- Với m = 1, do ![]() và q = 3 nên n 4
và q = 3 nên n 4
+) Khi n = 4 thì p > 2 nên p {4;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi n5: Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó pm,n,q nên p có 7 cách chọn. Ta được 35 số thỏa mãn.
- Với m2 tức là có 7 cách chọn m từ tập {2;4;5;6;7;8;9}. Khi đó ![]() với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và npm, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
với mọi n,p thuộc tập hợp {0;1;2;4;5;6;7;8;9} và npm, do đó có 8 cách chọn n, có 7 cách chọn p. Ta được 7.8.7 = 392 số thỏa mãn
2) M là số có 5 chữ số có dạng Khi đó: 14285 và r = 3
Do 14285 nên m chỉ nhận giá trị bằng 1 và n4
- Với m=1; n = 0,2 thì p,q là các số tùy ý thuộc tập {0;2;4;5;6;7;8;9} và pqn Ta được 2.7.6 = 84 số thỏa mãn.
- Với m=1; n = 4:
+) Khi p = 0 thì q là số tùy ý thuộc tập {2;5;6;7;8;9}. Ta được 6 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;5;6;7;8}. Ta được 5 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 6 + 35 + 392 + 84 + 6 + 5 = 528
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng

Câu 25:
Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử của A là = 3024 số.
Số phần tử của không gian mẫu là = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng ![]()
Theo bài ra ta có: ![]() và
và ![]()
Suy ra ![]()
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là ![]()
Chọn 2 cặp trong 4 cặp số trên để tạo số ![]()
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48
Câu 26:
Cho đa giác 30 đỉnh nội tiếp đường tròn, gọi (S) là tập hợp các đường thẳng đi qua hai trong số 30 đỉnh đã cho. Chọn 2 đường thẳng bất kỳ thuộc tập (S). Tính xác suất để chọn được 2 đường thẳng mà giao điểm của chúng nằm bên trong đường tròn.
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của (S) là số đường thẳng tạo nên từ 30 điểm đã cho là = 435
Số cách chọn 2 đường thẳng bất kỳ thuộc tập (S) là số phần tử không gian mẫu = = 94395
Giao điểm của hai đường thẳng nằm trong đường tròn tức là cũng nằm ở miền trong đa giác 30 đỉnh, khi đó giao điểm 2 đường thẳng cũng là giao điểm hai đường chéo của tứ giác có 4 đỉnh thuộc 30 đỉnh đa giác đã cho, vậy số giao điểm nằm trong đa giác chính là = 27405
Vậy xác suất cần tìm là ![]()
Câu 27:
Cho đa giác 30 đỉnh nội tiếp đường tròn, gọi (S) là tập hợp các đường thẳng đi qua hai trong số 30 đỉnh đã cho. Chọn 2 đường thẳng bất kỳ thuộc tập (S). Tính xác suất để chọn được 2 đường thẳng mà giao điểm của chúng nằm bên trong đường tròn.
 Xem đáp án
Xem đáp án
Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là - 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là ![]()
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
![]()
Câu 28:
Cho một đa giác đều có 20 đỉnh nội tiếp trong đường tròn (C). Lấy ngẫu nhiên hai đường chéo trong số các đường chéo của đa giác. Tính xác suất để lấy được hai đường chéo cắt nhau và giao điểm của hai đường chéo trong đường tròn?
 Xem đáp án
Xem đáp án
Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là - 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là ![]()
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
![]()
Câu 29:
Nhằm chào mừng ngày thành lập Đoàn TNCS Hồ Chí Minh, Đoàn trường THPT chuyên Lương Thế Vinh đã tổ chức giải bóng đá nam. Có 16 đội đăng kí tham dự trong đó có 3 đội: 10 Toán, 11 Toán, 12 Toán. Ban tổ chức cho bốc thăm ngẫu nhiên để chia đều 16 đội vào 4 bảng để đá vòng loại. Tính xác suất để 3 đội của 3 lớp Toán nằm ở bảng khác nhau.
 Xem đáp án
Xem đáp án
Chọn C
+ Chia đều 16 đội vào 4 bảng có ![]()
+ Sắp xếp 3 đội của 3 lớp Toán vào 3 bảng khác nhau trong 4 bảng có cách.
Chọn 3 đội trong 13 đội còn lại để xếp vào bảng có đội lớp 10 Toán có cách.
Chọn 3 đội trong 10 đội còn lại để xếp vào bảng có đội lớp 11 Toán có cách.
Chọn 3 đội trong 7 đội còn lại để xếp vào bảng có đội lớp 12 Toán có cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 16 đội vào 4 bảng sao cho 3 đội của 3 lớp Toán nằm ở 3 bảng khác nhau là ![]()
+ Xác suất cần tìm là: 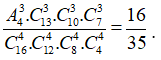
Câu 30:
Tung đồng thời 2 con súc sắc cân đối đồng chất. Gọi m là tích của số chấm trên hai con súc sắc trong mỗi lần tung. Tính xác suất để phương trình có hai nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Chọn D
Ta có số phần tử của không gian mẫu là = 36
Phương trình có hai nghiệm phân biệt khi và chỉ khi ![]()
Khi đó số chấm trên hai con con súc sắc là cặp số (i;j) với i,j = thỏa mãn
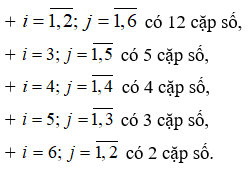
Như thế, có tất cả 12 + 5 + 4 + 3 +2 = 26 cặp số (i;j) để i.j = m < 18
Vậy xác suất cần tìm bằng
Câu 31:
Gọi X là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau. Lấy ngẫu nhiên một số thuộc tập X. Xác suất để số lấy được luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ.
 Xem đáp án
Xem đáp án
Chọn D
Gọi số có 6 chữ số có dạng ![]()
Từ 10 chữ số {0;1;2;3;4;5;6;7;8;9}, ta lập được 9. số có 6 chữ số đôi một khác nhau.
Lấy ngẫu nhiên một số từ tập X ![]()
Gọi A là biến cố “Lấy một số thuộc X luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ ”.
Ta coi 3 vị trí liền nhau trong X là một phần tử Z, sắp xếp 3 chữ số khác nhau trong Z thỏa mãn biến cố :
+ Số thứ nhất là số lẻ thuộc Y có 3 cách chọn.
+ Số thứ hai là số chẵn thuộc Y có 2 cách chọn.
+ Số thứ ba là số lẻ thuộc Y có 2 cách chọn.
Áp dụng quy tắc nhân ta có 12 cách sắp xếp phần tử .
Trường hợp 1: Số có 6 chữ số có dạng ![]()
+) z có 12 cách chọn.
+) Xếp 5 chữ số còn lại khác các số tập Y vào 3 vị trí ![]()
Áp dụng quy tắc nhân, ta lập được ![]()
Trường hợp2: Số có 6 chữ số có dạng ![]()
+) có 4 cách chọn ![]()
+) Xếp z vào 3 vị trí, z có 12 cách chọn nên có 36 cách sắp xếp.
+) Xếp 4chữ số còn lại vào 2 vị trí ![]()
Áp dụng quy tắc nhân, ta lập được 4.36. = 1728 số có 6 chữ số đôi một khác nhau thỏa mãn.
Vậy ta có tất cả ![]() (số) thoả mãn yêu cầu bài toán.
(số) thoả mãn yêu cầu bài toán.
![]()
Câu 32:
Trong một buổi dạ hội có 10 thành viên nam và 12 thành viên nữ, trong đó có 2 cặp vợ chồng. Ban tổ chức muốn chọn ra 7 đôi, mỗi đôi gồm 1 nam và 1 nữ để tham gia trò chơi. Tính xác suất để trong 7 đôi đó, có đúng một đôi là cặp vợ chồng. Biết rằng trong trò chơi, người vợ có thể ghép đôi với một người khác chồng mình và người chồng có thể ghép đôi với một người khác vợ mình
 Xem đáp án
Xem đáp án
Chọn B
Gọi 2 cặp vợ chồng là C1-V1 và C2-V2 (C=chồng, V=vợ).
* Số cách chọn ra 7 đôi:
- Đầu tiên chọn ra 7 nam trong 10 nam: (cách).
- Xếp 7 người nam này thành 1 hàng ngang, người đầu tiên có 12 cách ghép với nữ, người thứ hai có 11 cách, cứ như thế suy ra số cách ghép đôi là 12.11.10.9.8.7.6 (cách).
- Theo quy tắc nhân có 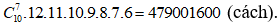
* Số cách chọn 7 đôi, chỉ có một cặp vợ chồng
- Trường hợp 1: chỉ có cặp vợ chồng C1-V1, khi đó lấy 6 nam trong 9 nam còn lại:
+ Nếu trong 6 nam này không có C2 thì số cách ghép 6 cặp còn lại là: ![]()
+ Nếu trong 6 nam này có C2 thì số cách ghép 6 cặp còn lại là: có 10 cách ghép C2 với nữ (trừ V2 và trừ V1), 5 nam còn lại có cách, số cách ghép cặp cho 5 nam này là 10.9.8.7.6 cách. Vậy theo quy tắc nhân có ![]()
Theo quy tắc cộng, có ![]()
- Trường hợp 2: chỉ có cặp vợ chồng C2-V2, tương tự như trên có 26248320(cách)
Vậy xác suất cần tính là: ![]()
Câu 33:
Chọn ngẫn nhiên ba số tự nhiên trong các số từ 101 đến 200. Tính xác suất để ba số đó lập thành một cấp số cộng có công sai dương.
 Xem đáp án
Xem đáp án
Chọn C
Ta có ![]()
Gọi , d lần lượt là số hạng đầu và công sai của cấp số cộng. Ta có các trường hợp sau:
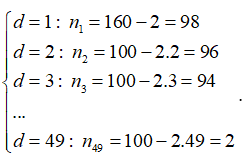
Suy ra số kết quả lấy ra 3 số lập thành cấp số cộng là
![]()
Vậy số cách chọn thỏa mãn đề bài là 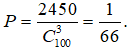
Câu 34:
Một nhóm học sinh gồm bốn bạn nam trong đó có bạn Quân và bốn bạn nữ trong đó có bạn Lan. Xếp ngẫu nhiên bốn bạn trên thành một hàng dọc. Xác suất để xếp được hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau bằng
 Xem đáp án
Xem đáp án
Chọn A
Ta đánh số các vị trí từ 1 đến 8.
Số phần tử không gian mẫu là ![]()
Gọi A là biến cố: “xếp được tám bạn thành hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau”.
TH1: Quân đứng vị trí 1 hoặc 8 => có 2 cách
Chọn một trong 3 bạn nam xếp vào vị trí 8 hoặc 1 còn lại => có 3 cách.
Xếp 2 bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau
=> có 6 cách
Xếp vị trí bạn Lan có 3 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: 2.3.6.3.3! = 648 cách
TH2: Chọn 2 bạn nam ( khác Quân) đứng vào 2 vị trí 1 hoặc 8 có cách.
Xếp Quân và bạn nam còn lại vào 2 trong 4 vị trí 3,4,5,6 mà 2 nam không đứng cạnh nhau => có 6 cách
Xếp vị trí bạn Lan có 2 cách.
Xếp 3 bạn nữ vào 3 vị trí còn lại có 3! cách.
=> TH này có: ![]()
![]()
Vậy xác suất của biến cố A là ![]()
Câu 35:
Cho tập hợp (S). Hai bạn A, B mỗi bạn chọn ngẫu nhiên một tập con của (S). Xác suất để tập con của A và B chọn được có đúng 2 phần tử chung gần nhất với kết quả nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn B
Số tập con của S là = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là:
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử ![]()
Khi đó: A có cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có cách chọn.
Vậy có: cách chọn tập con thỏa mãn.
Ta có điều kiện:
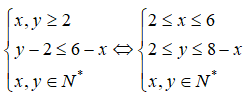
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:

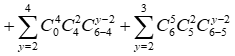
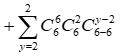
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: 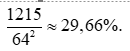
Câu 36:
Cho S là tập tất cả các số tự nhiên có 7 chữ số, lấy ngẫu nhiên một số từ tập S. Xác suất để số lấy được có chữ số tận cùng bằng 3 và chia hết cho 7 có kết quả gần nhất với số nào trong các số sau
 Xem đáp án
Xem đáp án
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó ![]()
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà 90000 = 70x128571 + 30, nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
|
9999973 |
9999983 |
9999993 |
|
Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra ![]()
Câu 37:
Cho một đa giác đều 48 đỉnh. Lấy ngẫu nhiên 3 đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.
 Xem đáp án
Xem đáp án
Chọn C
Số cách chọn ra 3 đỉnh tùy ý từ 48 đỉnh của đa giác là ![]()
Gọi A là biến cố “tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn”.
* Tính số tam giác tù
+ Chọn đỉnh thứ nhất có 48 cách chọn.
+ Để tạo thành tam giác tù thì ba đỉnh của tam giác phải thuộc cùng nửa đường tròn ngoại tiếp tam giác. Trong đỉnh còn lại sẽ có đỉnh cùng với đỉnh đã chọn thuộc cùng một nửa đường tròn ngoại tiếp. Nên số tam giác tù tạo thành là 48(tam giác).
* Tính số tam giác vuông tạo thành
+ Có 24 đường chéo đi qua tâm đường tròn ngoại tiếp tam giác.
+ Mỗi đường chéo trên cùng với 46 đỉnh còn lại tạ thành 46 tam giác vuông. Nên số tam giác vuông tạo thành là 24.46 = 1104(tam giác).
Do đó:
![]()

Câu 38:
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là
 Xem đáp án
Xem đáp án
Chọn C
Ta có: ![]()
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
![]()
TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
![]()

Câu 39:
Có hai dãy ghế đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng:
 Xem đáp án
Xem đáp án
Chọn A.
Số phần tử của không gian mẫu là n(W =) 6!.
Gọi A là biến cố : "Các bạn học sinh nam ngồi đối diện các bạn nữ".
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
Theo quy tắc nhân ta có cách
Câu 40:
Gọi S là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc tập S. Xác suất để số được chọn chia hết cho 3 là
 Xem đáp án
Xem đáp án
Chọn A
Gọi số có 9 chữ số có dạng ![]()
Từ 10 chữ số {0;1;2;3;4;5;6;7;8;9}, ta lập được số có 9 chữ số đôi một khác nhau.
Chọn ngẫu nhiên một số từ tập S ![]()
Gọi A là biến cố “Số được chọn chia hết cho 3”.
Đặt T = ![]()
Để ![]() (số có tổng các chữ số chia hết cho 3 sẽ chia hết cho 3)
(số có tổng các chữ số chia hết cho 3 sẽ chia hết cho 3)
Trường hợp 1: T = 45 => Số có 9 chữ số được lập từ các chữ số {1;2;3;4;5;6;7;8;9}
=> Lập được 9! số có 9 chữ số đôi một khác nhau và chia hết cho 3.
Trường hợp 2: T = 42 => Số có 9 chữ số được lập từ các chữ số {0;1;2;3;4;5;6;7;8;9}
+ có 8 cách chọn
+ Xếp 8 chữ số còn lại vào 8 vị trí có ![]()
Áp dụng quy tắc nhân, ta lập được số có 9 chữ số đôi một khác nhau và chia hết cho 3.
Trường hợp 3: T = 39 => Số có 9 chữ số được lập từ các chữ số {01;2;3;4;5;6;7;8;9}
Trường hợp 4:T = 36 => Số có 9 chữ số được lập từ các chữ số {0;1;2;3;4;5;6;7;8}
Trường hợp T = 39 và T = 36 tương tự như trường hợp T = 42
Vậy ta có tất cả 9! + 3.8.(8!) = 1330560 (số) thoả mãn yêu cầu bài toán
=> n(A) = 1330560