299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P4)
-
3307 lượt thi
-
40 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ?
 Xem đáp án
Xem đáp án
Chọn A
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}.
Ta có,
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng ¯abcde (a có thể bằng 0) là ![]() .
.
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng ¯0bcde là ![]()
Suy ra, số các số tự nhiên thỏa đề ra là ![]() .
.
Ý tưởng phát triển câu 39: thêm ràng buộc về thứ tự sắp xếp cho số tự nhiên lập được.
Câu 2:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn đứng liền nhau?
 Xem đáp án
Xem đáp án
Chọn D
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
¯abcde (a có thể bằng 0), đồng thời ba chữ số chẵn đứng liền nhau là ![]()
(để ý: có 3 cách xếp sao cho ba chữ số chẵn đứng liền nhau là ![]()
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng ¯0bcde, đồng thời ba chữ số chẵn đứng liền nhau là ![]()
(để ý: có 1 cách xếp sao cho hai chữ số chẵn còn lại đứng liền với số 0 là {b;c})
Suy ra, số các số tự nhiên thỏa đề ra là ![]()
Câu 3:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời hai chữ số lẻ đứng liền nhau?
 Xem đáp án
Xem đáp án
Chọn B.
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng ¯abcde (a có thể bằng 0), đồng thời hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 4 cách xếp sao cho hai chữ số lẻ đứng liền nhau là ![]()
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng ¯0bcde, đồng thời hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 3 cách xếp sao cho hai chữ số lẻ đứng liền nhau là ![]()
Suy ra, số các số tự nhiên thỏa đề ra là ![]()
Câu 4:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn đứng liền nhau và hai chữ số lẻ đứng liền nhau?
 Xem đáp án
Xem đáp án
Chọn A
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng ¯abcde (a có thể bằng 0), đồng thời ba chữ số chẵn đứng liền nhau, hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 2 cách xếp 3 chữ số chẵn thỏa đề {a,b,c}, {c,d,e})
+ Số các tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng ¯0bcde, đồng thời ba chữ số chẵn đứng liền nhau, hai chữ số lẻ đứng liền nhau là ![]()
(để ý: có 1 cách xếp sao cho hai chữ số chẵn còn lại đứng liền với số 0 là {b,c}).
Suy ra, số các số tự nhiên thỏa đề ra là ![]()
Câu 5:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn và hai chữ số lẻ đứng xen kẽ?
 Xem đáp án
Xem đáp án
Chọn C
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng ¯abcde (a có thể bằng 0), có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn và hai chữ số lẻ đứng xen kẽ là ![]()
(để ý: có 1 cách xếp 3 chữ số chẵn thỏa đề {a,c,e}).
+ Số các số tự nhiên có 5 chữ số đôi một khác nhau thỏa đề có dạng ¯0bcde, có đúng 3 chữ số chẵn và 2 chữ số lẻ, đồng thời ba chữ số chẵn và hai chữ số lẻ đứng xen kẽ là ![]()
(để ý: có 1 cách xếp 3 chữ số chẵn thỏa đề {0,c,e}).
Suy ra, số các số tự nhiên thỏa đề ra là ![]()
Câu 6:
Từ các chữ số thuộc tập X = {0;1;2;3;4;5;6;7} có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
 Xem đáp án
Xem đáp án
Chọn C
Giả sử số lập được có dạng ![]()
![]()
Ta có 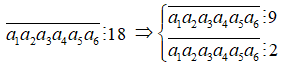
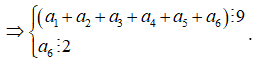
Vì ![]() nên ta có các trường hợp sau
nên ta có các trường hợp sau
Trường hợp 1: a1, được chọn từ ![]()
+ Có 3 cách chọn chọn
+ Có 5! cách chọn chọn bộ 5 số ![]()
Suy ra có 3.5! = 360 số.
Trường hợp 2: được chọn từ ![]()
+ = 0, có 5! cách chọn bộ 5 số ![]()
+ 0 khi đó có 3 cách chọn, có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 3.4.4!= 408 số
Trường hợp 3: được chọn từ ![]()
+ = 0, có 5! cách chọn bộ 5 số ![]()
+ 0 khi đó có 1 cách chọn, có 4 cách chọn và có 4! cách chọn bộ 4 số ![]()
Suy ra có 5! + 1.4.4! = 216 số
Vậy có: 360 + 408 + 216 = 984 số.
Câu 7:
Cho tập hợp S có 12 phần tử. Hỏi có bao nhiêu cách chia tập hợp S thành hai tập con (không kể thứ tự) mà hợp của chúng bằng S ?
 Xem đáp án
Xem đáp án
Chọn A
Cách 1.
Giả sử ![]() Đặt
Đặt ![]() Khi đó , C là ba tập con không giao nhau của S và S =
Khi đó , C là ba tập con không giao nhau của S và S =
Khi đó mỗi phần tử xS có 3 khả năng: Hoặc thuộc tập hoặc thuộc tập hoặc thuộc tập C.
Do đó 12 phần tử sẽ có cách chọn.
Trong các cách chọn nói trên có 1 trường hợp , C = S
Các trường hợp còn lại thì lặp lại 2 lần (đổi vai trò và cho nhau).
Do đó số cách chia là 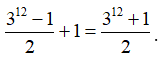
Cách 2.
Đặt S =
Nếu có k phần tử ![]()
![]()
![]()
![]()
Vậy số cách chọn 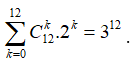
Nhưng trường hợp ![]() giống nhau và không hoán vị nên có
giống nhau và không hoán vị nên có 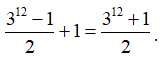 cách
cách
Câu 8:
Trong mặt phẳng cho 18 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác có các đỉnh thuộc 18 điểm đã cho là
 Xem đáp án
Xem đáp án
Chọn A
Ta chọn bất kì 3 điểm trong 18 điểm đã cho thì tạo thành một tam giác.
Do đó số tam giác được tạo thành là số cách chọn 3 điểm phân biệt bất kỳ (không kể thứ tự) từ 18 điểm đã cho.
Vậy có tất tam giác.
Câu 9:
Trong mặt phẳng cho 10 điểm phân biệt. Số vectơ khác , có điểm đầu và điểm cuối lấy trong các điểm đã cho là
 Xem đáp án
Xem đáp án
Chọn B
Số vectơ khác , có điểm đầu và điểm cuối lấy từ 10 điểm phân biệt trong mặt phẳng là
Câu 10:
Một lớp có 33 học sinh, cần chọn ra 6 học sinh để trực trường vào buổi chiều. Hỏi có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Chọn B
Mỗi cách chọn ra 6 học sinh trong 33 học sinh để trực trường là một tổ hợp chập 6 của 33 phần tử. Nên số cách chọn là cách.
Câu 11:
Một hộp đựng 20 viên bi khác nhau được đánh số từ 1 đến 20. Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại. Hỏi có bao nhiêu cách lấy để kết quả thu được là một số chia hết cho 3?
 Xem đáp án
Xem đáp án
Chọn C
20 viên bi khác nhau được đánh số từ 1 đến 20, chia làm ba phần:
Phần 1 gồm các viên bi mang số chia hết cho 3, có 6viên.
Phần 2 gồm các viên bi mang số chia cho 3 dư 1, có 7 viên.
Phần 3 gồm các viên bi mang số chia cho 3 dư 2, có 7 viên.
Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại, được một số chia hết cho 3 có các trường hợp sau:
Trường hợp 1: lấy được 3 viên bi ở phần 1, có cách.
Trường hợp 2: lấy được 3 viên bi ở phần 2, có cách.
Trường hợp 3: lấy được 3 viên bi ở phần 3, có cách.
Trường hợp 4: lấy được 1 viên bi ở phần 1, 1 viên bi ở phần 2 và 1 viên bi ở phần 3, có cách.
Vậy có ![]() cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.
cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.
Câu 12:
Có bao nhiêu đường thẳng cắt Hypebol y = tại hai điểm phân biệt mà cả hai điểm đó đều có tọa độ nguyên ?
 Xem đáp án
Xem đáp án
Chọn C
Ta có: 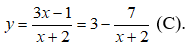
Tất cả các điểm có tọa độ nguyên thuộc (C) là: ![]()
Dễ thấy 4 điểm A, B, C, D không có 3 điểm nào thẳng hàng.
Suy ra lập được = 6 đường thẳng đi qua 2 trong 4 điểm đó.
Câu 13:
Trên bảng ô vuông của một bảng 4x4 ô vuông, người ta điền một trong hai số 6 hoặc -6 sao cho tổng các số trong mỗi hàng và trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách điền như thế? (tham khảo hình vẽ ví dụ cho một trường hợp điền số thỏa mãn yêu cầu)
|
|
-6 |
-6 |
6 |
|
6 |
-6 |
-6 |
6 |
|
-6 |
6 |
6 |
-6 |
|
-6 |
6 |
6 |
-6 |
 Xem đáp án
Xem đáp án
Chọn C
Để cho tiện lặp luận, ta thay việc điền số 6 ta nói là điền dấu cộng "+" và thay cho việc điền số -6 ta nói là điền dấu trừ "-" . Theo thứ tự từ hàng trên xuống ta gọi là hàng 1, 2, 3, 4. Vậy mỗi hàng và mỗi cột ta cần điền 2 dấu "+" và 2 dấu "-"
Xét hai hàng 1 và 2, ta có các trường hợp sau:
Trường hợp 1: Cách điền các dấu "+", "-" ở hai hàng 1 và 2 không có 2 ô tương ứng theo cột nào giống nhau. Nói cách khác, hai hàng 1 và 2 có điền dấu trái ngược nhau. Khi đó, số cách điền dấu ở hàng 1 là 4C2 = 6, hàng 2 chỉ có một cách điền ngược lại. Tổng dấu ở hai ô tương ứng theo cột của hai hàng đầu bằng 0 nên đến hàng thứ 3 ta điền 2 dấu "+" và 2 dấu "-" tùy ý. Hàng thứ tư chỉ có cách điền ngược dấu với hàng thứ ba. Vậy có 4C2 = 6 cách điền dấu hai hàng cuối. Trong trường hợp này ta có 6.6 = 36 cách điền số thỏa mãn đề bài.
Trường hợp 2: Cách điền các dấu "+", "-" ở hai hàng 1 và 2 có cả 4 ô tương ứng theo cột giống nhau. Khi đó, số cách điền dấu ở hàng một và hai là 4C2 = 6. Tổng dấu ở 2 ô tương ứng theo cột của 2 hàng đầu bằng hai lần dấu "+" hoặc 2 lần dấu "-"nên đến hàng thứ ba, tư ta điền dấu giống nhau và ngược lại so với hàng một, hai. Vậy chỉ có một cách điền dấu hai hàng cuối. Trong trường hợp này ta có 6 cách điền số thỏa mãn đề bài.
Trường hợp 3: Cách điền các dấu "+", "-" ở hai hàng một và hai có đúng hai ô tương ứng theo cột giống nhau. Tức là có đúng hai cột giống nhau và 2 cột khác nhau.
Chọn một trong hai cột giống nhau để điền dấu "+", cột giống nhau còn lại điền dấu "-" thì có 2 cách. Ở hai cột khác nhau cũng chỉ có 2 cách điền dấu ngược nhau. Đến hàng thứ ba, ở cột ô giống nhau của hai hàng trên, ta chỉ có cách điền ngược dấu, còn ở cột ô khác nhau, ta có cách điền tùy ý dấu nào cũng được, nhưng chỉ được tùy ý cho 2 cách điền ở một ô, ô còn lại không có lựa chọn. Vậy có 2 cách điền hàng ba. Hàng thứ tư chỉ có một cách điền duy nhất.
Vậy trong trường hợp này ta có 6.4.2 48 cách.
Tóm lại có 36 + 6 + 48 = 90 cách.
Câu 14:
Với k và n là hai số nguyên dương tùy ý thỏa mãn kn, mệnh đề nào dưới đây đúng ?
 Xem đáp án
Xem đáp án
Chọn A
Câu 15:
Số các hoán vị của 4 phần tử là
 Xem đáp án
Xem đáp án
Chọn A
Số các hoán vị của 4 phần tử là = 4! = 24.
Câu 16:
Sắp xếp 20 người vào 2 bàn tròn A, B phân biệt, mỗi bàn gồm 10 chỗ ngồi. Số cách sắp xếp là
 Xem đáp án
Xem đáp án
Chọn A
Giả sử khi xếp 10 người vào một bàn tròn, hai cách sắp xếp được xem là như nhau nếu cách này nhận được từ cách kia bằng cách xoay bàn đi một góc nào đó.
Bài toán trên được chia thành các công đoạn sau:
Công đoạn 1: Chọn 10 người trong 20 người đã cho để xếp vào bàn tròn A: có cách.
Công đoạn 2: Sắp xếp 10 người vừa chọn được ở công đoạn 1 vào bàn tròn A: có 9! cách.
Công đoạn 3: Sắp xếp 10 người còn lại vào bàn tròn B: có 9! cách.
Vậy số cách sắp xếp là: .9!.9! cách.
Câu 17:
Số cách chọn ra 3 học sinh trong số 10 học sinh không tính thứ tự là
 Xem đáp án
Xem đáp án
Chọn B
Số cách chọn ra 3 học sinh trong số 10 học sinh không tính thứ tự là = 120 cách.
Câu 18:
Cho một hình vuông có cạnh bằng 4. Chia hình vuông này thành 16 hình vuông đơn vị có cạnh bằng 1. Hỏi có bao nhiêu tam giác có các đỉnh là các đỉnh của hình vuông đơn vị?
 Xem đáp án
Xem đáp án
Chọn B
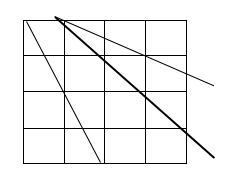
Số cách chọn ra 3 đỉnh trong số 25 đỉnh của các hình vuông đơn vị là:
TH1: 3 đỉnh nằm trên cùng 1 hàng hoặc cùng 1 cột là: 5 + 5
TH2: 3 đỉnh nằm trên một trong các đường chéo của hình vuông kích thước 4x4, 3x3, 2x2 sao cho các đường chéo ấy không trùng nhau là ![]()
TH3: 3 đỉnh nằm trên một trong các đường chéo của hình chữ nhật kích thước 2x4. Số hình chữ nhật đó là 6. Do đó số cách chọn là 12
Vậy số tam giác được tạo thành là ![]() = 2148
= 2148
Câu 19:
Tập giá trị của hàm số y = là
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện xác định: 3x7
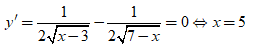
Ta có: ![]() mà hàm số y = liên tục trên [3;7], suy ra
mà hàm số y = liên tục trên [3;7], suy ra
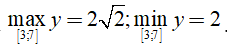
Vậy tập giá trị của hàm số là [2;]
Câu 20:
Cho k, n (k < n) là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn B
Ta có ![]() nên B đúng.
nên B đúng.
Câu 21:
Trong mệnh đề sau, mệnh để nào sai?
 Xem đáp án
Xem đáp án
Chọn D
Áp dụng công thức: ![]() suy ra đáp án sai là
suy ra đáp án sai là
Câu 22:
Tìm tất cả các giá trị của n thỏa mãn .
 Xem đáp án
Xem đáp án
Chọn B
Điều kiện: ![]()
Ta có ![]()
![]()
![]()
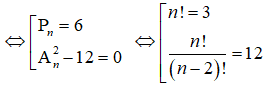
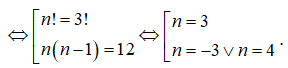
So với điều kiện, các giá trị cần tìm là n = 3; n = 4
Câu 23:
Biết . Ta có bằng
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện : ![]()
ta có:![]()
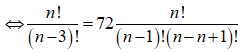
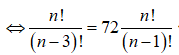

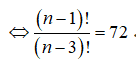
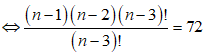
![]()
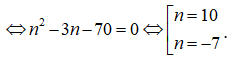
Kết hợp với điều kiện (*) suy ra n = 10
Khi đó 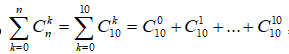
![]()
Câu 24:
Cho số tự nhiên n thỏa mãn . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn C
Phương pháp: Sử dụng các công thức 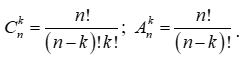
Giải: Điều kiện: n 2.
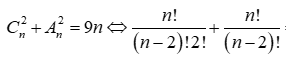
![]()
![]()
Câu 25:
Cuối năm học trường Chuyên Sư phạm tổ chức 3 tiết mục văn nghệ chia tay khối 12 ra trường. Tất cả các học sinh lớp 12A đều tham gia nhưng mỗi người chỉ được đăng kí không quá 2 tiết mục. Biết lớp 12A có 44 học sinh, hỏi có bao nhiêu cách để lớp lựa chọn?
 Xem đáp án
Xem đáp án
Chọn D
Vì mỗi học sinh lớp 12A được đăng kí 1 hoặc 2 tiết mục trong số 3 tiết mục văn nghệ nên số cách lựa chọn tiết mục văn nghệ của mỗi học sinh là: = 6.
Lớp 12A có 44 học sinh đều tham gia văn nghệ nên số cách để lớp lựa chọn là: .
Câu 27:
Tổng S = bằng
 Xem đáp án
Xem đáp án
Chọn A
+ Xét trong tập số phức ta có:

Đặt 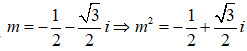
![]()
+ Ta có ![]()
+ Xét khai triển ![]()
![]()
+ Lần lượt thay x = 1, x = m và x = vào (*) ta được :
![]()
![]()
![]()
![]()
![]()
![]()
+ Cộng theo từng vế (1), (2), (3) ta được: ![]()
+ Mà ![]()
![]()
Vậy ta có ![]()
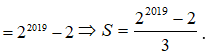
Câu 28:
Tìm nN biết khai triển nhị thức 2 có tất cả 15 số hạng.
 Xem đáp án
Xem đáp án
Chọn B
Khai triển có tất cả 15 số hạng tức là n + 4 = 14 => n = 10
Câu 29:
Trong khai triển nhị thức có tất cả 19 số hạng. Vậy n bằng
 Xem đáp án
Xem đáp án
Chọn B
Số các số hạng của khai triển nhị thức Newton của là n+1 số hạng.
Do đó ta có: n + 6 = 18 => n = 12.
Câu 30:
Khai triển nhị thức
 Xem đáp án
Xem đáp án
Chọn B.
Khai triển nhị thức ![]() thì có n + 1 số hạng nên khai triển nhị thức
thì có n + 1 số hạng nên khai triển nhị thức
Câu 31:
Có bao nhiêu số hạng trong khai triển nhị thức thành đa thức.
 Xem đáp án
Xem đáp án
Chọn B
![]()
![]()
![]()
Vậy khai triển trên có 2019 số hạng.
Câu 32:
Cho khai triển . Tính tổng các hệ số trong khai triển?
 Xem đáp án
Xem đáp án
Chọn B
Ta có ![]()
![]()
Tổng các hệ số trong khai triển là: ![]()
Cho x = 1 ta có: ![]()
![]()
![]()
![]()
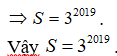
Câu 33:
Cho T(x) = . Sau khi khai triển và rút gọn T(x) có bao nhiêu số hạng?
 Xem đáp án
Xem đáp án
Chọn D
Ta có
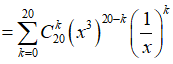
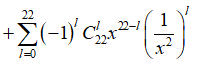
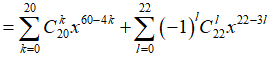
Các số hạng có số mũ của x trùng nhau khi ![]() với
với ![]()
![]() suy ra các hệ số của số hạng có mũ x trùng nhau luôn dương nên trong T(x), các số hạng có số mũ x trùng nhau không bị triệt tiêu.
suy ra các hệ số của số hạng có mũ x trùng nhau luôn dương nên trong T(x), các số hạng có số mũ x trùng nhau không bị triệt tiêu.
Mặt khác, 4k - 3 = 38 ![]() với
với ![]()
Từ (2) => m lẻ

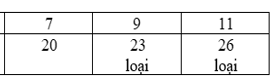
Suy ra trong khai triển trên có 4 số hạng có số mũ của x trùng nhau. Vậy sau khi khai triển và rút gọn T(x) có 21 + 23 - 4 =40 số hạng.
Câu 34:
Có bao nhiêu hạng tử là số nguyên trong khai triển ?
 Xem đáp án
Xem đáp án
Chọn A
Theo công thức khai triển nhị thức Newton ta có:

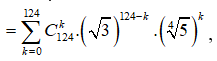
![]()
Suy ra số hạng tổng quát (k+1) trong khai triển là: ![]()
Hạng tử là số nguyên trong khai triển ứng với k thỏa mãn:
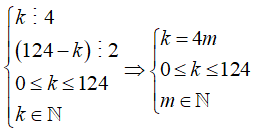
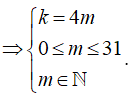
Suy ra có 32 giá trị k thỏa mãn. Do đó có 32 hạng tử là số nguyên trong khai triển 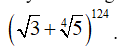
Câu 35:
Hệ số của số hạng chứa trong khai triển ( với x 0) bằng
 Xem đáp án
Xem đáp án
Chọn B
Ta xét khai triển ( với x 0) có số hạng tổng quát là
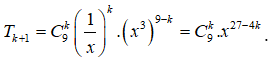 .
.
Số hạng chứa tương ứng với giá trị k thỏa mãn: 27 - 4k = 3 => k = 6.
Vậy hệ số của số hạng chứa là = 84.
Câu 36:
Hệ số của trong khai triển nhị thức bằng
 Xem đáp án
Xem đáp án
Chọn C
Ta có 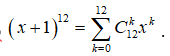 . Hệ số của ứng với k = 7 là .
. Hệ số của ứng với k = 7 là .
Câu 37:
Cho số nguyên dương n và hệ số của trong khai triển Newton của bằng 31.Khi đó n bằng
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
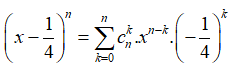
Vì hệ số của trong khai triển Newton của bằng 31 nên ta có:
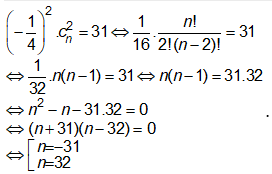
Vì n nguyên dương nên n = 32
Câu 38:
Cho số nguyên dương n và hệ số của trong khai triển Newton của bằng 459. Khi đó n bằng:![]()
 Xem đáp án
Xem đáp án
Chọn A
Câu 39:
Trong khai triển biết tổng các hệ số . Hệ số của bằng
 Xem đáp án
Xem đáp án
Chọn C
Ghi nhớ: Với khai triển nhị thức:
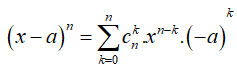
(Với a0 là hằng số) thì hệ số của ![]()
Câu 40:
Tìm hệ số của số hạng không chứa x trong khai triển .
 Xem đáp án
Xem đáp án
Chọn C
Ta có: 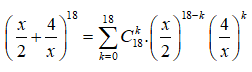

![]()
Số hạng tổng quát trong khai triển ![]()
![]()
Số hạng không chứa x trong khai triển phải có: ![]()
=> 18 - 2k = 0 => k = 9
Suy ra hệ số của số hạng không chứa x trong khai triển là: ![]()
