299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P9)
-
3304 lượt thi
-
40 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trên đường tròn đặt 24 điểm cách đều nhau sao cho độ dài cung giữa 2 điểm kề nhau đều bằng 1. Chọn ngẫu nhiên 8 trong 24 điểm đó. Tính xác suất sao cho trong 8 điểm được chọn không có 2 điểm nào có độ dài cung bằng 8 hoặc 3.
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử không gian mẫu ![]()
Gọi biến cố A = “Chọn 8 điểm sao cho không có 2 điểm nào có độ dài cung bằng 8 hoặc 3”.
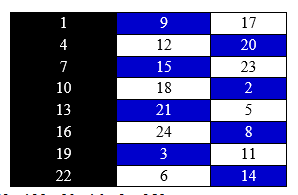
Chia 24 điểm của đường tròn thành bảng sau:
|
1 |
9 |
17 |
|
4 |
12 |
20 |
|
7 |
15 |
23 |
|
10 |
18 |
2 |
|
13 |
21 |
5 |
|
16 |
24 |
8 |
|
19 |
3 |
11 |
|
22 |
6 |
14 |
Trong đó, mỗi cột là tập các số có cùng số dư khi chia 3, mỗi hàng là tập các số có cùng số dư khi chia 8. Nhận thấy, mỗi cột không được chọn quá 4 số vì chọn từ 5 số trở lên, sẽ xuất hiện 2 số kề nhau tạo cung có độ dài là 3.
TH1: Chọn 4 số của cột 1 không kề nhau: 2 cách là {1;7;13;19} hoặc {4;10;16;22}
|
1 |
9 |
17 |
|
4 |
12 |
20 |
|
7 |
15 |
23 |
|
10 |
18 |
2 |
|
13 |
21 |
5 |
|
16 |
24 |
8 |
|
19 |
3 |
11 |
|
22 |
6 |
14 |
Tiếp theo, chọn 4 số a,b,c,d còn lại không nằm cùng hàng với 4 số của cột 1 và 2 số bất kỳ trong 4 số a,b,c,d cũng không được cùng hàng với nhau, có cách chọn.
Vậy có 2.= 32cách.
TH2: Chọn 3 số của cột 1 sao cho không có 2 số nào kề nhau: ![]()
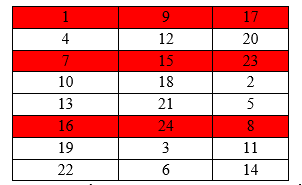
VD chọn{1;7;16} thì 5 số còn lai sẽ thuộc 3 nhóm màu trắng như hình vẽ. Khi đó mỗi nhóm màu trắng trong bảng chỉ có 2 cách chọn. Do đó TH2 có 16.2.2.2=128 cách.
TH3: Chọn 2 số không kề nhau của cột 1: - 8 = 20
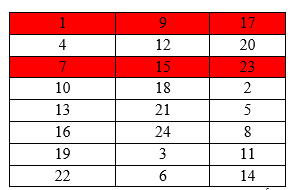
Khi đó, 6 hàng ngang còn lai chia làm 2 nhóm màu trắng như hình vẽ. Mỗi nhóm có đúng 2 cách chọn nên có 20.2.2 = 80 cách.
TH4: Chọn 1 số của cột 1 có 8 cách
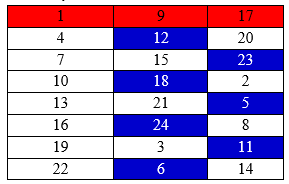
TH5: Chỉ chọn cột 2 với 3. Ta có 2 cách chọn là các dòng xanh hoặc trắng: 2 cách.
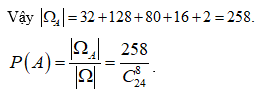
Câu 2:
Ông Hùng muốn mở két sắt của mình nhưng ông quên mất mật mã két. Biết rằng mã két gồm 4 chữ số khác 0 và có tổng của 4 chữ số đó bằng 10. Tính xác suất để ông ấy mở được két sắt ở lượt bấm thứ nhất.
 Xem đáp án
Xem đáp án
Chọn A
Gọi là số có 4 chữ số sao cho a,b,c,d khác 0 và a + b + c + d = 10.
Số cách chọn 4 chữ số chính là số cách “dùng 3 “vách ngăn” chèn vào giữa các chữ số 1 (như ví dụ bên dưới) để chia thành 4 phần”.
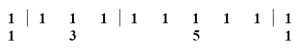
Suy ra có = 84 cách, tương ứng có 84 số thỏa mãn.
Vậy xác suất để ông Hùng mở được két sắt ở lượt bấm thứ nhất là P =
Câu 3:
Hai mươi lăm em học sinh lớp 12A được xếp ngồi vào một vòng tròn trong đêm lửa trại. Ba em học sinh được chọn ( xác suất được lựa chọn đối với mỗi em là như nhau ) và cử tham gia một trò chơi. Xác suất để ít nhất hai trong ba em học sinh được chọn ngồi cạnh nhau là
 Xem đáp án
Xem đáp án
Chọn A
Gọi A là biến cố chọn được 3 em học sinh mà ít nhất 2 em trong đó ngồi cạnh nhau.
là biến cố chọn được 3 em học sinh ngồi cạnh nhau.
là biến cố chọn được 3 em học sinh mà trong đó chỉ có 2 em ngồi cạnh nhau.
![]()
Số phương án chọn ra 3 em từ 25 em là :![]() (cách).
(cách).
Nhận thấy khi xét về 1 chiều, cứ 1 học sinh sẽ có duy nhất 1 học sinh khác ngồi cạnh. Việc đổi chiều sẽ tạo ra các phương án trùng lặp. Vậy để chọn ra 2 em ngồi cạnh nhau ta có: 25 (cách).
Số phương án để chọn ra 3 học sinh ngồi cạnh nhau cũng tương tự và có là: = 25 (cách).
Số phương án chọn học sinh thứ 3 sao cho học sinh này không ngồi cạnh 2 bạn kia là: 21(cách).
Số phương án chọn 3 học sinh sao cho có 2 em ngồi cạnh nhau là = 25.21 = 525(cách).
Vậy xác suất xảy ra A là: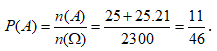
Câu 4:
Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 7 quyển sách Tiếng Anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không ở cạnh nhau
 Xem đáp án
Xem đáp án
Chọn A
|
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
Gọi là biến cố “xếp quyển sách lên kệ sách một cách tùy ý”
=> n() = 14!
A là biến cố “xếp 14 cuốn sách lên kệ sách sao cho hai cuốn sách cùng môn không ở cạnh nhau”.
- Xếp quyển sách Tiếng Anh vào kệ có 7! cách.
- quyển sách Tiếng Anh tạo ra 8 chỗ trống (gồm 6 chỗ trống ở giữa và 2 chỗ trống trước sau).
Đánh số từ 1 đến 8, từ trái sang phải cho các chỗ trống. Khi đó ta xét các trường hợp:
TH1: Xếp sách Văn hoặc Toán vào vị trí từ 1 đến 7 có 7! cách.
TH2: Xếp sách Văn hoặc Toán vào vị trí từ 2 đến 8 có 7! cách.
TH3: Xếp cặp sách Văn – Toán chung vào ngăn, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại. Ta có:
+ Số cách chọn cặp sách Văn – Toán: 3.4 cách.
+ Vị trí 2 cuốn sách trong cặp sách: 2! cách.
+ Xếp các sách còn lại vào các ngăn 3,4,5,6,7 có 5! cách
Vậy ta có số cách xếp 1 cặp sách Văn – Toán chung vào ngăn 2, các ngăn 3,4,5,6,7 xếp tùy ý số sách còn lại là 3.4.2!.5! cách.
Tương tự cho xếp cặp sách Văn – Toán lần lượt vào các ngăn 3,4,5,6,7
Số trường hợp thuận lợi của biến cố là ![]()
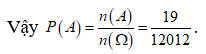
Câu 5:
Một lớp có 20 học sinh nữ và 25 học sinh nam. Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác tham gia một hoạt động của Đoàn trường. Xác suất để 4 học sinh được chọn có cả nam và nữ bằng (làm tròn đến chữ số thập phân thứ 4)
 Xem đáp án
Xem đáp án
Chọn C
Gọi A: “4 học sinh được chọn có cả nam và nữ.”
=> : “4 học sinh được chọn chỉ có nam hoặc chỉ có nữ.”
Số cách để lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác:
Số cách chọn 4 học sinh toàn là nam:
Số cách chọn 4 học sinh toàn là nữ:
Xác suất để 4 học sinh được chọn có cả nam và nữ:
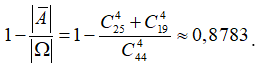
Câu 6:
Bạn Nam làm bài thi thử THPT Quốc gia môn Toán có 50 câu, mỗi câu có 4 đáp án khác nhau, mỗi câu đúng được 0,2 điểm, mỗi câu làm sai hoặc không làm không được điểm cũng không bị trừ điểm. Bạn Nam đã làm đúng được 40 câu còn 10 câu còn lại bạn chọn ngẫu nhiên mỗi câu một đáp án. Xác suất để bạn Nam được trên điểm gần với số nào nhất trong các số sau?
 Xem đáp án
Xem đáp án
Chọn A
Vì mỗi câu có 4 phương án trả lời và chỉ có một phương án đúng nên xác suất để chọn đúng đáp án là , xác suất để trả lời sai là
Gọi là biến cố bạn Nam được trên 8,5 điểm thì là biến cố bạn Nam được dưới 8,5 điểm
Vì bạn Nam đã làm chắc chắn đúng 40c âu nên để có xảy ra 2 trường hợp
TH1: Bạn Nam chọn được một câu đúng trong 10 câu còn lại, xác suất xảy ra là:
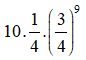
TH2: Bạn Nam chọn được hai câu đúng trong 10 câu còn lại, xác suất xảy ra là:
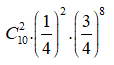
Vậy ![]()
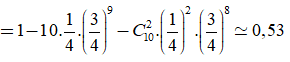
Câu 7:
Một lô hàng gồm 30 sản phẩm trong đó có 20 sản phẩm tốt và 10 sản phẩm xấu. Lấy ngẫu nhiên 3 sản phẩm trong lô hàng. Tính xác suất để 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt.
 Xem đáp án
Xem đáp án
Chọn D
Ta có: ![]()
Gọi A là biến cố lấy ra 3 sản phẩm trong đó có ít nhất một sản phẩm tốt.
=> là biến cố lấy ra 3 sản phẩm không có sản phẩm tốt và ![]()
Vậy 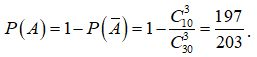
Câu 8:
Một hộp kín chứa 50 quả bóng kích thước bằng nhau, được đánh số từ 1 đến 50. Bốc ngẫu nhiên cùng lúc 2 quả bóng từ hộp trên. Gọi P là xác suất bốc được 2 quả bóng có tích của 2 số ghi trên 2quả bóng là một số chia hết cho 10, khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn C
![]() .
.
Gọi là biến cố “bốc được quả bóng có tích của số ghi trên quả bóng là một số chia hết cho 10 ”. Xét các tập hợp sau:
![]()
 Tập có 20 phần tử.
Tập có 20 phần tử.
![]()
Có ba trường hợp xảy ra khi tích của hai số trên hai quả bóng chia hết cho 10.
Trường hợp 1: 1 quả bóng có số ghi thuộc tập , quả bóng còn lại có số ghi thuộc tập B\
Khi đó số cách bốc 2 quả bóng là: ![]() (cách).
(cách).
Trường hợp 2: 2 quả bóng có số ghi đều thuộc tập .
Khi đó số cách bốc 2 quả bóng là: (cách).
Trường hợp 3: 1 quả bóng có số ghi thuộc tập , quả bóng còn lại có số ghi thuộc tập .
Khi đó số cách bốc 2 quả bóng là: ![]()
Suy ra: ![]()
Vậy:
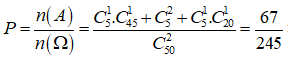
=> 0,25 < P < 0,3
Câu 9:
Một lô hàng có 20 sản phầm, trong đó có 2 sản phẩm bị lỗi còn lại là sản phẩm tốt. Lấy ngẫu nhiên 4 sản phẩm từ lô hàng đó để kiểm tra. Tính xác suất để trong 4 sản phẩm lấy ra có sản phẩm lỗi.
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử không gian mấu bằng số cách lấy ra 4 sản phẩm từ 20 sản phẩm là: (cách)
Cách 1: Để lấy ra 4 sản phẩm có sản phẩm lỗi ta chia các trường hợp:
TH1: Lấy được 3 sản phẩm tốt và 1 sản phẩm lỗi, ta có: (cách)
TH2: Lấy được 2 sản phẩm tốt và 2 sản phẩm lỗi, ta có: (cách)
Vậy xác suất cần tìm là: 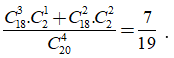
Cách 2: Xét biến cố đối:
Số cách lấy ra 4 sản phẩm không có sản phẩm lỗi (cách)
Vậy xác suất cần tìm là: 
Câu 10:
Xếp ngẫu nhiên 5 bạn An, Bình, Cường, Dũng, Đông ngồi vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Xác suất của biến cố “hai bạn An và Bình không ngồi cạnh nhau” là:
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử của không gian mẫu: = 5!
Gọi A:”Hai bạn An và Bình không ngồi cạnh nhau”
Thì :”Hai bạn An và Bình ngồi cạnh nhau”
Xếp An và Bình ngồi cạnh nhau coi như 1 phần tử
- Xếp 1 phần tử (An+Bình) và 3 bạn còn lại theo các thứ tự khác nhau có: 4! Cách
- Xếp 2 học sinh An và Bình ngồi cạnh nhau có 2! cách
Suy ra 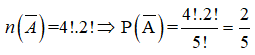
Câu 11:
Một lớp có 20 học sinh nữ và 25 học sinh nam. Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác tham gia một hoạt động của Đoàn trường. Xác suất để 4 học sinh được chọn có cả nam và nữ bằng (làm tròn đến chữ số thập phân thứ 4).
 Xem đáp án
Xem đáp án
Chọn C
CÁCH 1
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: ![]()
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ”.
Ta xét các trường hợp:
TH1: Chọn được 1 nữ, 3 nam. Số cách chọn là: ![]()
TH2: Chọn được 2 nữ, 2 nam. Số cách chọn là: ![]() .
.
TH3: Chọn được 3 nữ, 1 nam. Số cách chọn là: ![]() .
.
Suy ra ![]()
Vậy xác suất cần tìm là: ![]()
CÁCH 2
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: ![]()
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ” thì là biến cố: “cả 4 học sinh được chọn chỉ có nam hoặc nữ”.
Ta có ![]()
Do đó xác suất xảy ra của biến cố là: 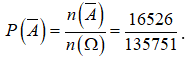
Suy ra ![]()
Câu 12:
Gọi X là tập hợp tất cả các số tự nhiên có 8 chữ số được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Lấy ngẫu nhiên một số trong tập hợp X. Gọi A là biến cố lấy được số có đúng hai chữ số 1, có đúng hai chữ số 2, bốn chữ số còn lại đôi một khác nhau, đồng thời các chữ số giống nhau không đứng liền kề nhau. Xác suất của biến cố A bằng
 Xem đáp án
Xem đáp án
Chọn D
*) Ta có: ![]()
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có ![]() (cách).
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có ![]() cách.
cách.
Xếp hai chữ số 2 đứng liền nhau: Có ![]() cách.
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: ![]() (cách)
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: ![]() (cách)
(cách)
Vậy ![]()
Câu 13:
Một hộp chứa 10 quả cầu đỏ được đánh số từ 1 đến 10, 20 quả cầu xanh được đánh số từ 1 đến 20. Lấy ngẫu nhiên một quả. Khi đó xác suất để lấy được quả màu xanh hoặc ghi số lẻ bằng
 Xem đáp án
Xem đáp án
Chọn D
Chọn ngẫu nhiên một quả trong 30 quả có 30 cách. Vậy = 30.
Gọi A là biến cố: “lấy được quả cầu màu xanh”.
Ta có n(A) = 20 => P(A) =
Gọi B là biến cố: “lấy được quả cầu ghi số lẻ”.
Ta có n(B) = 15 => P(B) = .
Số quả cầu vừa màu xanh vừa ghi số lẻ: 10 (quả).
Xác suất để lấy được quả cầu vừa màu xanh vừa ghi số lẻ: 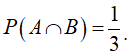
Xác suất để lấy được quả cầu màu xanh hay ghi số lẻ:
![]()
![]()
Câu 14:
Một hộp chứa 15 quả cầu đỏ được đánh số từ 1 đến 15, 20 quả cầu xanh được đánh số từ 1 đến 20. Lấy ngẫu nhiên đồng thời hai quả. Khi đó xác suất để hai quả cầu lấy được đều màu đỏ hoặc đều ghi số chẵn bằng
 Xem đáp án
Xem đáp án
Chọn D
Câu 15:
Trong ngày hội trại xuân, cô giáo chủ nhiệm tổ chức cho một nhóm 30 bạn trong lớp tham gia hai tiết mục văn nghệ là tốp ca và tốp nhảy flashmob. Có 12 bạn tham gia tốp ca, 15 bạn tham gia nhảy flashmob và 6 bạn tham gia cả hai tiết mục. Chọn 1 bạn học sinh bất kì trong lớp, tính xác suất để bạn học sinh này tham gia ít nhất một trong hai tiết mục văn nghệ đã nêu.
 Xem đáp án
Xem đáp án
Chọn A
Ghi nhớ: Công thức cộng xác suất: ![]()
Câu 16:
Tại Giải vô địch bóng đá Đông Nam Á 2018 (AFF Suzuki Cup 2018) có 10 đội tuyển tham dự, trong đó có đội tuyển Việt Nam và đội tuyển Malaysia. Ở vòng bảng, Ban tổ chức chia ngẫu nhiên 10 đội thành 2 bảng, bảng A và bảng B, mỗi bảng có 5 đội. Giả sử khả năng xếp mỗi đội vào mỗi bảng là như nhau. Tính xác suất để đội Việt Nam và đội tuyển Malaysia được xếp trong cùng một bảng.
 Xem đáp án
Xem đáp án
Chọn A
Gọi A là biến cố “Đội tuyển Việt Nam và đội tuyển Malaysia được xếp trong cùng một bảng”.
Ta có: ![]() .
.
Do đó: 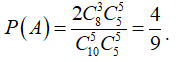 .
.
Câu 17:
Sắp xếp 5 quyển sách Toán và 4 quyển sách Văn lên một kệ sách dài. Tính xác suất để các quyển sách cùng một môn nằm cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn C
Số cách xếp 9 quyển sách lên một kệ sách dài là 9! . Suy ra số phần tử không gian mẫu: = 9!
Gọi A là biến cố: “các quyển sách cùng một môn nằm cạnh nhau”.
Ta xếp các cuốn sách cùng một bộ môn thành một nhóm
Trước hết ta xếp 2 nhóm lên kệ sách chúng ta có: 2! cách xếp
Với mỗi cách xếp 2 nhóm đó lên kệ ta có 5! cách hoán vị các cuốn sách Toán và 4! cách hoán vị các cuốn sách Văn. Suy ra n(A) = 5!.4!.2!
Xác suất cần tìm là 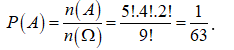
Câu 18:
Giải bóng chuyền quốc tế VTV Cup có 12 đội tham gia, trong đó có 3 đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành 3 bảng đấu, mỗi bảng 4 đội. Tính xác suất để 3 đội của Việt Nam cùng nằm ở một bảng đấu.
 Xem đáp án
Xem đáp án
Chọn D
Gọi A là biến cố “3 đội của Việt Nam cùng nằm ở một bảng đấu”.
Ta có ![]()
Chọn ra 3 đội của Việt Nam và 1 đội khác rồi xếp chung vào 1 trong 3 bảng có: 3. (cách).
Chọn ra 4 đội trong 8 đội còn lại để được bảng tiếp theo có: (cách).
Bảng còn lại có 1 cách chọn.
![]()
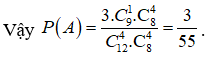
Câu 19:
Có 2 học sinh lớp A, 3 học sinh lớp B và 4 học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh lớp B. Hỏi có bao nhiêu cách sắp xếp như vậy?
 Xem đáp án
Xem đáp án
Chọn C
Để xếp 9 em học sinh thành một hàng dọc ta thực hiện ba hành động liên tiếp
* Sắp xếp 3 học sinh lớp B. Có 3! cách.
* Sắp xếp 2 học sinh lớp A đứng cạnh các học sinh lớp B sao cho giữa hai học sinh lớp A không có học sinh lớp B. Có .2! cách.
* Lần lượt sắp xếp 4 học sinh lớp C còn lại đứng cạnh các học sinh trên. Có cách.
Vậy có tất cả 3!.2!.
Bình luận: Trong đề thi thử THPT chuyên Thái Nguyên lần 2 trong câu hỏi này không có đáp án 145152 mà thay bởi đáp án 145112. Tôi thiết nghĩ lỗi do người làm đề đã đánh máy nên đã tự ý đổi lại một đáp án khác mà tôi nghĩ chính xác hơn.
Câu 20:
Trước kì thi học sinh giỏi, nhà trường tổ chức buổi gặp mặt 10 em học sinh trong đội tuyển. Biết các em đó có số thứ tự trong danh sách lập thành cấp số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ được ngồi một học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau.
 Xem đáp án
Xem đáp án
Chọn C.
Giả sử số thứ tự trong danh sách là ![]()
Do dãy này là cấp số cộng nên ta có ![]()
![]() .
.
Số phần tử của không gian mẫu là = 10!
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự 5 cặp học sinh có các cặp số thứ tự là![]()
![]() vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
vào trước 5 cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước 1. Bước này có cách.
Suy ra số kết quả thuận lợi cho biến cố A là 5!..
Vậy xác suất của biến cố A là ![]()
Câu 21:
Xếp chỗ cho 6 học sinh trong đó có học sinh A và 3 thầy giáo vào 9 ghế kê thành hàng ngang (mỗi ghế xếp một người). Tính xác suất sao cho mỗi thầy giáo ngồi giữa 2 học sinh và học sinh A ngồi ở một trong hai đầu hàng.
 Xem đáp án
Xem đáp án
Chọn B
Xếp 9 người vào 9 ghế kê hàng ngang ta có: =9! cách sắp xếp.
Gọi B là biến cố để “mỗi thầy giáo ngồi giữa 2 học sinh và học sinh A ngồi ở một trong hai đầu hàng.”
Theo đề, học sinh A ngồi ở một trong hai đầu hàng nên có 2 cách sắp xếp.
Xếp 5 học sinh còn lại vào 5 vị trí có 5! cách sắp xếp. Xem mỗi học sinh tạo thành một vách ngăn tạo thành 5 khoảng trống. Xếp 3 thầy vào 5 khoảng trống có cách.
![]() cách.
cách.
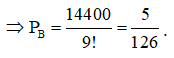
Câu 22:
Một bàn dài có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Người ta muốn xếp chỗ ngồi cho 5học sinh trường X và 5 học sinh trường Y vào bàn nói trên. Tính xác suất để bất cứ hai học sinh nào ngồi đối diện nhau đều khác trường với nhau.
 Xem đáp án
Xem đáp án
Chọn C
![]()
Ta có số phần tử không gian mẫu: = 10!.
+) Có 10 cách chọn học sinh cho vị trí số 1. Với mỗi cách chọn vị trí số 1 có 5 cách chọn học sinh cho vị trí số 10 ( Nếu vị trí số 1 là học sinh X thì có 5 cách chọn học sinh ở vị trí 10 là học sinh Y và ngược lại).
+) Có 8 cách chọn học sinh cho vị trí số 2 ( Loại 2 học sinh ở vị trí 10) . Với mỗi cách chọn vị trí số 2 có 4 cách chọn học sinh cho vị trí số 9( Nếu vị trí số 2 là X thì có 4 cách chọn vị trí số 9 là Y, chỉ còn 4 do đã loại 1 em ở lần chọn trước).
+) Hoàn toàn tương tự cho đến hết ta được số phần tử của biến cố cần tính xác suất là: ![]()
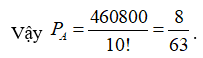
Câu 23:
Có 4 người xếp thành hàng ngang và mỗi người gieo 1 đồng xu cân đối đồng chất. Xác suất để tồn tại hai người cạnh nhau có cùng kết quả là
 Xem đáp án
Xem đáp án
Chọn A
![]() Gọi A là biến cố tồn tại 2 người cạnh nhau có cùng kết quả.
Gọi A là biến cố tồn tại 2 người cạnh nhau có cùng kết quả.
=> là biến cố không tồn tại 2 người cạnh nhau không cùng kết quả.
Các trường hợp của ![]() là : S-N-S-N hoặc N-S-N-S.
là : S-N-S-N hoặc N-S-N-S.
![]() .
.
Ta có: ![]()
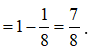 .
.
Câu 24:
Một chiếc hộp đựng 5 viên bi trắng, 3 viên bi xanh và 4 viên bi vàng. Lấy ngẫu nhiên 4 viên bi từ hộp đó. Tính xác suất để lấy ra 4 viên bi có đủ ba màu.
 Xem đáp án
Xem đáp án
Chọn D
Cách 1:
Số phần tử của không gian mẫu: ![]() .
.
Gọi A là biến cố: “lấy ra 4 viên bi có đủ ba màu”
Ta xét các khả năng của biến cố A:
TH1: Lấy được 1 bi trắng, 1 bi xanh và 2 bi vàng, trường hợp này có ![]() (cách).
(cách).
TH2: Lấy được 1 bi trắng, 2 bi xanh và 1 bi vàng, trường hợp này có ![]() (cách).
(cách).
TH3: Lấy được 2 bi trắng, 1 bi xanh và 1 bi vàng, trường hợp này có ![]() (cách).
(cách).
Số cách lấy 4 viên bi có đủ cả ba màu là: ![]()
Xác suất cần tìm là ![]()
Cách 2:
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “lấy ra 4 viên bi không có đủ ba màu” .
Ta có: ![]()
Xác suất của biến cố A là: ![]()
Vậy xác suất cần tìm là: 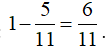 .
.
Câu 25:
Lớp 11A có 2 tổ. Tổ I có 5 bạn nam, 3 bạn nữ và tổ II có 4 bạn nam, 4 bạn nữ. Lấy ngẫu nhiên mỗi tổ 2 bạn đi lao động. Tính xác suất để trong các bạn đi lao động có đúng 3 bạn nữ.
 Xem đáp án
Xem đáp án
Chọn B
Chọn mỗi tổ 2 bạn nên số phần tử của không gian mẫu ![]() .
.
Gọi A là biến cố : “Có đúng 3 bạn nữ trong 4 bạn đi lao động”, khi đó
TH1: Chọn 2 nữ tổ I, 1 nữ tổ II, 1 nam tổ II có ![]() .
.
TH2: Chọn 2 nữ tổ II, 1 nữ tổ I, 1 nam tổ I có ![]() .
.
Suy ra ![]() .
.
Xác suất để chọn 4 bạn đi lao động có đúng 3 bạn nữ là ![]() .
.
Câu 26:
Một hội nghị gồm 6 đại biểu nước Anh, 7 đại biểu nước Pháp và 7 đại biểu nước Nga, trong đó mỗi nước có 2 đại biểu là nam. Chọn ngẫu nhiên ra 4 đại biểu. Xác suất chọn được 4 đại biểu để trong đó mỗi nước đều có ít nhất một đại biểu và có cả đại biểu nam và đại biểu nữ bằng
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu ![]()
Gọi A là biến cố: “chọn được 4 đại biểu để trong đó mỗi nước đều có 1 đại biểu và có cả đại biểu
nam và đại biểu nữ”
Số cách chọn 4 người đủ các nước tức là có một nước có 2 người, hai nước còn lại, mỗi nước 1 người là:.
![]()
Số cách chọn 4 người đủ các nước và toàn đại biểu nam là:
![]()
Số cách chọn 4 người đủ các nước và toàn đại biểu nữ là:
![]()
Số phần tử của A là n(A) = 2499- 12 - 550 = 1937
Xác suất của biến cố A: ![]()
Câu 27:
Đội thanh niên xung kích của một trường THPT gồm 15 học sinh trong đó có 4 học sinh khối 12, 5 học sinh khối 11 và 6 học sinh khối 10. Chọn ngẫu nhiên ra 6 học sinh đi làm nhiệm vụ. Tính xác suất để chọn được 6 học sinh đủ 3 khối.
 Xem đáp án
Xem đáp án
Chọn D
Số cách chọn 6 học sinh từ 15 học sinh là = 5005(cách)
= 5005
Gọi biến cố A: “Chọn được 6 học sinh đủ 3 khối”
=> : “Chọn được 6 học sinh không đủ 3 khối”.
Cách 1
+ Trường hợp 1: Chọn 6 học sinh từ 1 khối 1 => Chọn 6 học sinh khối 10 có = 1 (cách).
+ Trường hợp 2: 6 học sinh được chọn trong 2 khối.
* Chọn 6 học sinh trong khối 11 và khối 12 có ![]() (cách).
(cách).
* Chọn 6 học sinh trong khối 10 và khối 12 có ![]() (cách)
(cách)
* Chọn 6 học sinh trong khối 11 và khối 10 có ![]() (cách).
(cách).
Từ 2 trường hợp suy ra ![]()
.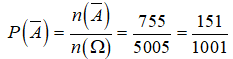
 0
0
Cách 2
+ Trường hợp 1: Chọn 6 học sinh từ 1 khối => Chọn 6 học sinh khối 10 có = 1 (cách).
+ Trường hợp 2: 6 học sinh được chọn trong 2 khối có ![]()
Từ 2 trường hợp suy ra ![]()
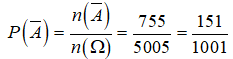
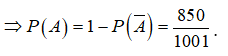
Câu 28:
Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4 nữ, ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau bằng
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu là số cách sắp xếp 8 học sinh vào 8 chỗ ngồi khác nhau. Suy ra = 8!
Gọi A là biến cố xếp 8 học sinh sao cho mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau. Ta đánh số các chỗ ngồi từ 1 đến 8 như sau:
Dãy 1:
|
1 |
2 |
3 |
4 |
Dãy 2:
|
8 |
7 |
6 |
5 |
Để sắp xếp các học sinh ngồi vào vị trí thỏa mãn yêu cầu bài toán ta sắp xếp như sau:
Trường hợp 1: 4 học sinh nam ngồi vào các số lẻ, 4 học sinh nữ ngồi vào các số chẵn. Trường hợp này có 4!4! cách.
Trường hợp 2: 4 học sinh nam ngồi vào các số chẵn, 4 học sinh nữ ngồi vào các số lẻ. Trường hợp này có 414! cách.
Do đó n(A) = 2.4!.4!
Vậy xác suất của biến cố A là 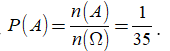
Câu 29:
Đội tuyển học sinh giỏi Toán 12 của trường THPT X có 7 học sinh trong đó có bạn Minh Anh. Lực học của các học sinh là như nhau. Nhà trường chọn ngẫu nhiên 4 học sinh đi thi. Tìm xác suất để Minh Anh được chọn đi thi.
 Xem đáp án
Xem đáp án
Chọn B
Không gian mẫu =
Gọi biến cố A: “Minh Anh được chọn trong 4 học sinh được chọn đi thi.”
+ Chọn Minh Anh đi thi có 1 cách.
+ Chọn 3 bạn trong 6 bạn còn lại có cách.
Suy ra n(A) = 1. = 20
Vậy xác suất để Minh Anh được chọn đi thi là:  .
.
Câu 30:
Trong Lễ tổng kết Tháng thanh niên, có 10 đoàn viên xuất sắc gồm 5 nam và 5 nữ được tuyên dương khen thưởng. Các đoàn viên này được sắp xếp ngẫu nhiên thành một hàng ngang trên sân khấu để nhận giấy khen. Tính xác suất để trong hàng ngang trên không có bất kì bạn nữ nào đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn B
Gọi là không gian mẫu. Ta có: = 10!.
Gọi A là biến cố: “Xếp 10 bạn thành một hàng ngang không có bất kì bạn nữ nào đứng cạnh nhau”.
![]() Xếp ngẫu nhiên 5 bạn nam vào 5 vị trí có 5! cách.
Xếp ngẫu nhiên 5 bạn nam vào 5 vị trí có 5! cách.
![]() Xếp 5 bạn nữ xen vào giữa 4 khoảng trống giữa 5 bạn nam, vị trí đầu và cuối hàng có cách.
Xếp 5 bạn nữ xen vào giữa 4 khoảng trống giữa 5 bạn nam, vị trí đầu và cuối hàng có cách.
![]()
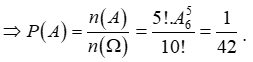
* Phân tích bài toán
- Bài toán trên dùng phương pháp tạo vách ngăn để giải quyết.
- Nội dung của phương pháp.
Sắp xếp m đối tượng khác nhau thuộc nhóm 1 và n đối tượng khác nhau thuộc nhóm 2 vào m+n (m > n) vị trí khác nhau sao cho thỏa mãn không có hai vật nhóm 2 nào đứng cạnh nhau.
- Cách giải:
+ Bước 1: Sắp xếp m vào m vị trí sẽ tạo ra m+1 vách ngăn.
+ Bước 2: Sắp xếp n đối tượng còn lại theo yêu càu bài toán vào m+1 vách ngăn vừa tạo.
Câu 31:
Có 4 quyển sách Toán, 6 quyển sách Lý và 8 quyển sách Hóa khác nhau được xếp lên giá sách theo một hàng ngang. Tính xác suất để không có bất kỳ hai quyển sách Hóa đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn D
Gọi là không gian mẫu. Ta có: n() = 18!.
Gọi A là biến cố: “Xếp 18 quyển sách lên giá sách theo một hàng ngang sao cho không có bất kỳ hai quyển sách Hóa đứng cạnh nhau”.
![]() Xếp ngẫu nhiên 10 quyển sách gồm 4 quyển sách Toán và 6 quyển sách Lý vào 10 vị trí có 10! cách.
Xếp ngẫu nhiên 10 quyển sách gồm 4 quyển sách Toán và 6 quyển sách Lý vào 10 vị trí có 10! cách.
![]() Xếp 8 quyển sách Hóa vào 9 khoảng trống giữa 10 quyển sách Toán và Lý, vị trí đầu và cuối giá sách có cách.
Xếp 8 quyển sách Hóa vào 9 khoảng trống giữa 10 quyển sách Toán và Lý, vị trí đầu và cuối giá sách có cách.
=> n(A) = 10!.
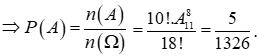
Câu 32:
Người ta sắp xếp ngẫu nhiên 5 viên bi được đánh số từ 1 đến 5 vào năm chiếc hộp theo một hàng ngang. Tính xác suất để các viên bi được đánh số chẵn luôn đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn B
Gọi là không gian mẫu. Ta có: n() = 5!.
Gọi A là biến cố: “Xếp 5 viên bi được đánh số từ 1 đến 5 vào năm chiếc hộp sao cho các viên bi được đánh số chẵn nằm trong các hộp đứng cạnh nhau ”.
![]() Xếp 2 viên bi có đánh số chẵn (viên bi số 2 và viên bi số 4) vào 2 hộp đứng cạnh nhau có 2! cách.
Xếp 2 viên bi có đánh số chẵn (viên bi số 2 và viên bi số 4) vào 2 hộp đứng cạnh nhau có 2! cách.
![]() Ta coi việc xếp 2 viên bi chẵn vào hai chiếc hộp đứng cạnh nhau là xếp chúng vào một chiếc hộp lớn.
Ta coi việc xếp 2 viên bi chẵn vào hai chiếc hộp đứng cạnh nhau là xếp chúng vào một chiếc hộp lớn.
![]() Xếp 3 viên bi có đánh số lẻ (viên bi số 1, viên bi số 3 và viên bi số 5) vào 3 chiếc hộp và 2 viên bi đánh số chẵn (viên bi số 2 và viên bi số 4) vào 1 chiếc hộp lớn nên ta có 4 chiếc hộp để sắp xếp, vậy có 4! cách.
Xếp 3 viên bi có đánh số lẻ (viên bi số 1, viên bi số 3 và viên bi số 5) vào 3 chiếc hộp và 2 viên bi đánh số chẵn (viên bi số 2 và viên bi số 4) vào 1 chiếc hộp lớn nên ta có 4 chiếc hộp để sắp xếp, vậy có 4! cách.
Vậy n(A) = 2!.4!
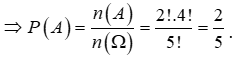
Câu 33:
Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp A, 3 học sinh lớp B và 5 học sinh lớp C thành một hàng ngang. Xác suất để không có học sinh lớp B nào xếp giữa hai học sinh lớp A bằng
 Xem đáp án
Xem đáp án
Chọn C
Số cách xếp ngẫu nhiên là 10! cách.
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn ![]() học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có cách, ta được một nhóm X.
học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có cách, ta được một nhóm X.
* Xếp ![]() học sinh còn lại với nhóm X có (9-k)! cách.
học sinh còn lại với nhóm X có (9-k)! cách.
Vậy tất cả có 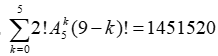 cách xếp thỏa mãn.
cách xếp thỏa mãn.
Xác suất cần tính bằng ![]()
Câu 34:
Có 3 quyển sách toán, 4 quyển sách lí và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách gồm có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong ba ngăn (mỗi ngăn đủ rộng để chứa tất cả quyển sách). Tính xác suất để không có bất kì hai quyển sách toán nào đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn D
Giá có 3 ngăn như vậy có 2 vách ngăn, coi 2 vách ngăn này là 2 quyển sách giống nhau. Khi đó
bài toán trở thành xếp 14 quyển sách (2 quyển “VÁCH NGĂN” giống nhau) vào 14 vị trí. Đầu
tiên chọn 2 vị trị trí xếp vách ngăn là , 12 vị trí còn lại xếp 12 quyển sách là 12!. Vậy không gian mẫu là .12!.
Gọi A là biến cố “không có bất kì hai quyển sách toán nào đứng cạnh nhau”. Ta tìm số cách xếp thỏa mãn A
Đầu tiên ta xếp 11 quyển sách gồm 4 quyển lí, 5 quyển hóa và 2 quyển “VÁCH NGĂN”. Cũng
như trên, ta chọn 2 vị trí xếp 2 quyển “VÁCH NGĂN” trước là sau đó xếp 9 quyển còn lại là 9!. Vậy số cách xếp 11 quyển này là .9!. Sau khi xếp xong 11 quyển này thì sẽ có sẽ có 12 khe. Ta chọn 3 khe để xếp 3 quyển toán còn lại, là .
Vậy số cách thỏa mãn biến cố A là ..9!.
Vậy 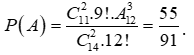 .
.
Câu 35:
Hai bạn Công và Thành cùng viết ngẫu nhiên ra một số tự nhiên gồm hai chữ số phân biệt. Xác suất để hai số được viết ra có ít nhất một chữ số chung bằng?
 Xem đáp án
Xem đáp án
Chọn C
Số các số tự nhiên có hai chữ số phân biệt là 9.9 = 81 số.
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố “Hai chữ số được viết ra có ít nhất một chữ số chung”
Khi đó ta có biến cố là “Hai chữ số được viết ra không có chữ số chung”
Gọi hai chữ số mà Công và Thành viết ra lần lượt là
- TH1: b = 0, khi đó a có 9 cách, c có 8 cách và d có 7 cách. Vậy có 9.8.7 = 504 cách viết.
- TH2: b 0, khi đó a có 9 cách, b có 8 cách, c có 7 cách và d có 7 cách. Vậy có 9.8.7.7 = 3528 cách viết.
![]() cách viết.
cách viết.
Vậy xác suất của biến cố A là:
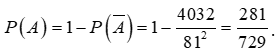
Nhận xét: Đây là một bài toán xác suất chọn số. Đối với bài toán này, ta sẽ đi theo hướng tính gián tiếp thông qua phần bù. Khi đó cách làm sẽ ngắn hơn và tránh nhầm lẫn không đáng có.
Câu 36:
Cho tập hợp 1;2;3;4;5;6. Chọn ngẫu nhiên 3 số từ tập S. Tính xác suất để 3 số được chọn lập thành một cấp số cộng.
 Xem đáp án
Xem đáp án
Chọn A
Ta có không gian mẫu là ![]()
Gọi A là biến cố “3 số được chọn lập thành một cấp số cộng”
Giả sử 3 số được chọn là a,b,c theo thứ tự lập thành cấp số cộng => a + c = 2b. Do đó a + c là một số chẵn nên a và c cùng chẵn hoặc cùng lẻ.
Chia S thành 2 tập ![]()
Ứng với mỗi cách chọn a và c thì chỉ có một cách chọn b tương ứng.
![]()
Vậy xác suất của biến cố A là
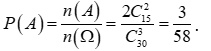
Câu 37:
Từ các số 1;2;3;4;5;6 lập được bao nhiêu số tự nhiên gồm tám chữ số sao cho trong mỗi số đó có đúng ba chữ số 1, các chữ số còn lại đôi một khác nhau và hai chữ số chẵn không đứng cạnh nhau?
 Xem đáp án
Xem đáp án
Chọn B
Bước 1: ta xếp các số lẻ: có các số lẻ là 1,1,3,5 vậy có cách xếp.
Bước 2: ta xếp 3 số chẵn 2, 4, 6 xen kẽ 5 số lẻ trên có 6 vị trí để xếp 3 số vậy có cách xếp.
Vậy có = 2400 số thỏa mãn yêu cầu bài toán.
Câu 38:
Một hội nghị gồm 6 đại biểu đến từ Việt Nam, 7 đại biểu đến từ Mỹ, 7 đại biểu đến từ Anh, trong đó mỗi Quốc gia có đúng 2 đại biểu nữ. Chọn ngẫu nhiên ra 4 đại biểu. Tính xác suất để chọn được 4 đại biểu sao cho mỗi Quốc gia đều có ít nhất 1 đại biểu và có cả đại biểu nam và nữ.
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của không gian mẫu là: ![]() .
.
Gọi A là biến cố “chọn được 4 đại biểu sao cho mỗi Quốc gia đều có ít nhất 1 đại biểu và có cả đại biểu nam và nữ.”
Trường hợp 1: có 2 đại biểu Việt Nam, 1 đại biểu Mỹ, 1 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 1 là: ![]() cách chọn.
cách chọn.
Trường hợp 2: Có 1 đại biểu Việt Nam, 2 đại biểu Mỹ,1 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 2 là:![]()
Trường hợp 3: Có 1 đại biểu Việt Nam, 1 đại biểu Mỹ, 2 đại biểu Anh.
Số cách chọn ra 4 đại biểu có cả đại biểu nam và đại biểu nữ thỏa mãn trường hợp 3 là: ![]() .
.
Nên tổng số cách chọn thỏa mãn yêu cầu là: 581 + 678 + 678 = 1937.
Vậy xác suất của biến cố A là: ![]() .
.
Câu 39:
Xếp ngẫu nhiên tám học sinh gồm bốn học sinh nam (trong đó có Hoàng và Nam) cùng bốn học sinh nữ (trong đó có Lan) thành một hàng ngang. Xác suất để trong tám học sinh trên không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Lan đứng cạnh Hoàng và Nam là
 Xem đáp án
Xem đáp án
Chọn D
Xếp ngẫu nhiên tám học sinh thành hàng ngang, có 8! cách. Suy ra = 8! = 40320
Gọi A là biến cố cần tính xác suất.
Ta coi Hoàng, Lan, Nam ( Lan ở giữa) là một nhóm. Khi đó vì hai bên nhóm này bắt buộc là nữ nên coi nhóm này là một nam. Vậy có thể coi ta có ba nam và ba nữ.
Khi đó có hai trường hợp xảy ra.
Trường hợp 1: Nam ngồi vị trí lẻ.
Xếp ba nam vào vị trí lẻ có 3! cách.
Xếp ba nữ vào vị trí chẵn có 3! cách.
Hoán vị hai học sinh nam trong nhóm ( Hoàng- Lan- Nam) có 2! cách.
Vậy số cách sắp xếp trong trường hợp này là 3!.3!.2! = 72 cách.
Trường hợp 2: Nam ngồi vị trí chẵn.
Tương tự trường hợp này có 3!.3!.2! = 72 cách.
Suy ra n(A) = 72 + 72 = 144 cách.
Vậy 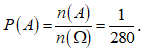
Câu 40:
Có 60 quả cầu được đánh số từ 1 đến 60. Lấy ngẫu nhiên đồng thời hai quả cầu rồi nhân các số trên hai quả cầu với nhau. Tính xác suất để tích nhận được là số chia hết cho 10.
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của không gian mẫu là: ![]() .
.
Gọi A: “ Biến cố lấy đồng thời ngẫu nhiên hai quả cầu sao cho tích của các số trên hai quả cầu chia hết cho 10”.
TH1: Hai quả cầu bốc được có chữ số tận cùng là 0 có (cách).
TH2: Hai quả cầu bốc được có 1 quả cầu có chữ số tận cùng là 0 có ![]() (cách).
(cách).
TH3: Hai quả cầu bốc được có 1 quả cầu có chữ số tận cùng là 5 và 1 quả cầu có chữ số tận cùng là 2,3,6,8 có ![]()
Khi đó số phần tử của biến cố A là ![]() .
.
Vậy xác suất của biến cố A là: