299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P10)
-
741 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Một nhóm gồm 3 học sinh lớp 10, 3 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngồi vào một hàng có 9 ghế, mỗi học sinh ngồi 1 ghế. Tính xác suất để 3 học sinh lớp 10 không ngồi 3 ghế liền nhau.
 Xem đáp án
Xem đáp án
Chọn D
Nhóm có tất cả 9 học sinh nên số cách xếp 9 học sinh này ngồi vào một hàng có 9 ghế là 9! = 362880(cách).
Vậy số phần tử không gian mẫu là = 362880
Đặt biến cố A: “ 3 học sinh lớp không ngồi ghế liền nhau”.
Giả sử học sinh lớp 10 ngồi 3 ghế liền nhau. Ta xem 3 học sinh này là một nhóm
+/ Xếp X và 6 bạn còn lại vào ghế có 7! cách xếp.
+/ Ứng với mỗi cách xếp ở trên, có 3! cách xếp các bạn trong nhóm X.
Vậy theo quy tắc nhân ta có số cách xếp là: 7!.3! = 30240 (cách).
Suy ra số cách xếp để học sinh lớp không ngồi cạnh nhau là (cách) .
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là 362880 - 30240 = 332640 (cách)
=> n(A) = 332640
Vậy xác suất để học sinh lớp 10 không ngồi cạnh nhau là
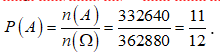
Câu 2:
Một nhóm có 8 học sinh gồm 4 bạn nam và 4 bạn nữ trong đó có 1 cặp sinh đôi gồm 1 nam và 1 nữ. Xếp ngẫu nhiên 8 học sinh này vào 2 dãy ghế đối diện, mỗi dãy 4 ghế, sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau bằng
 Xem đáp án
Xem đáp án
Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
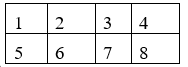
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
![]()
Câu 3:
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau. Gọi A là biến cố: “Lập được số mà tổng của ba chữ số thuộc hàng đơn vị, chục, trăm lớn hơn tổng của ba chữ số còn lại là 3 đơn vị”. Xác suất của biến cố A là:
 Xem đáp án
Xem đáp án
Chọn D
Từ các chữ số 1; 2; 3; 4; 5; 6 ta lập các số tự nhiên có 6 chữ số khác nhau, lập được 6! = 720 số. Vậy số phần tử của không gian mẫu là = 720 số
Gọi là số tự nhiên có 6 chữ số khác nhau thuộc biến cố A.
Ta có: 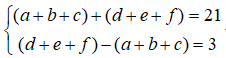
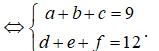
Từ sáu chữ số 1; 2; 3; 4; 5; 6 ta phân chia thành bộ ba số có tổng là 9 và bộ ba số có tổng là 12, có 3 cách phân chia, đó là (1;2;6) và (3;4;5), (1;3;5) và (2;4;6), (2;3;4) và (1;5;6). Trong mỗi cách phân chia này, ta lập được 3!.3! = 36 số. Do đó n(A) = 3.36 = 108.
Vậy xác suất của biến cố A là:
![]()
Câu 4:
Mỗi bạn An và Bình chọn ngẫu nhiên ba số trong tập {0,1,2,3,4,5,6,7,8,9}. Tính xác suất để trong hai bộ ba số của An và Bình chọn ra có nhiều nhất một số giống nhau bằng:
 Xem đáp án
Xem đáp án
Chọn C
Số cách chọn của An là ; số cách chọn của Bình là . Vậy số phần tử của không gian mẫu là: ![]()
Gọi A là biến cố “ Hai bộ ba số An và Bình chọn ra có nhiều nhất một số giống nhau”.
TH1: Không có số nào giống nhau thì có cách chọn.
TH2: Có một số giống nhau thì có cách chọn.
Do đó ![]()
Vậy xác suất cần tìm là:
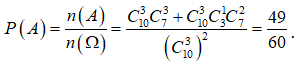
Câu 5:
Cho E là tập các số tự nhiên có 6 chữ số đôi một khác nhau lập được từ các số 0; 1; 2; 3; 4; 5; 6. Tính xác suất để chọn ngẫu nhiên từ E được một số có dạng sao cho a + b + c + d = e + f
 Xem đáp án
Xem đáp án
Chọn B
Số phần tử của tập hợp E là ![]()
Vì ![]()
![]()
Mà chia hết cho 3 nên khi lấy ra 6 chữ số thỏa điều kiện ta phải loại ra một số chia hết cho 3. Ta có 3 trường hợp sau:
1) Trường hợp 1:
Loại bỏ số 0, khi đó a + b = c + d = e + f = 7
Bước 1: Chia ra làm 3 cặp số có tổng bằng 7 là : (1;6), (2;5), (3;4) có 1 cách chia.
Bước 2: Chọn a có 6 cách; chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 6.1.4.1.2.1 = 48 cách.
Trường hợp này có 48 số.
2) Trường hợp 2:
Loại bỏ số 3, khi đó a + b = c + d = e + f = 6
Bước 1: Chia ra làm 3 cặp số có tổng bằng 6 là : (0;6), (1;5), (2;4) có 1 cách chia.
Bước 2: Chọn a có 5 cách (vì có số 0); chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 5.1.4.1.2.1 = 40 cách.
Trường hợp này có 40 số.
3) Trường hợp 3:
Loại bỏ số 6, khi đó a + b = c + d = e + f = 5. Tương tự như trường hợp 2, có 40 số.
Vậy trong tập hợp E có tất cả 48 + 40 + 40 = 128 số có dạng sao cho a + b = c + d = e + f
Xác suất cần tìm là: ![]()
Câu 6:
Gọi A là tập các số tự nhiên gồm 5 chữ số mà các chữ số đều khác 0. Lấy ngẫu nhiên từ tập A một số. Tính xác suất để lấy được số mà chỉ có đúng 3 chữ số khác nhau.
 Xem đáp án
Xem đáp án
Chọn C
Gọi x là số bi của hộp thứ nhất nên số bi ở hộp thứ hai là 20 - x ![]() )
)
Gọi a,b ![]() lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
Suy ra: 0 < a < x, 0 < b < 20 - x
Số cách lấy bi ở mỗi hộp là độc lập với nhau nên ta đặt:
+) Xác suất lấy một bi xanh ở hộp thứ nhất là và ở hộp thứ hai là
Với a, b, x là các số tự nhiên thỏa mãn ![]()
+) Xác suất lấy được hai bi xanh 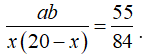
Ta có ![]()
![]()
Lập bảng thử từng giá trị
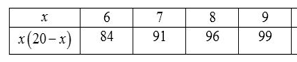
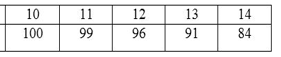
Khi đó, các giá trị của x là 6 hoặc 84
Ta lại có 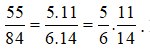
Do đó, ![]() hoặc ngược lại
hoặc ngược lại
Vậy xác suất để lấy được hai viên bi đỏ là
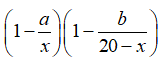
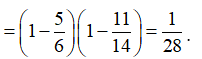
Câu 7:
Chọn ngẫu nhiên một số từ tập hợp tất cả các số tự nhiên gồm bốn chữ số phân biệt được lấy từ các chữ số 0,1,2,3,4,8,9. Tính xác suất để số được chọn lớn hơn số 2019 và bé hơn số 9102.
 Xem đáp án
Xem đáp án
Chọn C
Ta có: ![]()
Gọi B là biến cố cần tìm xác suất.
Số cách chọn 3 chữ số phân biệt a,b,c từ 9 chữ số khác 0 là
TH1. Có 1 chữ số trong 3 chữ số a,b,c được lặp 3 lần.
Chọn chữ số lặp: có 3 cách, giả sử là a.
Xếp 5 chữ số a,a,a,b,c có cách, (vì cứ 3! hoán vị của các vị trí mà a,a,a chiếm chỗ thì tạo ra cùng một số n).
Suy ra trong trường hợp này có  số tự nhiên.
số tự nhiên.
TH2. Có 2 trong 3 chữ số a,b,c mỗi chữ số được lặp 2 lần.
Chọn 2 chữ số lặp: có cách, giả sử là a, b.
Xếp 5 chữ số có a,a,b,b,c có cách, (vì cứ 2! hoán vị của các vị trí mà a,a chiếm chỗ và 2! hoán vị của các vị trí mà b,b chiếm chỗ thì tạo ra cùng một số n).
Suy ra trong trường hợp này có 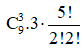 số tự nhiên.
số tự nhiên.
Do đó ta có 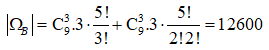 số
số
Kết luận: 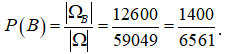
Cách 2: Lưu Thêm
Gọi A là tập các số tự nhiên gồm chữ số mà các chữ số đều khác 0.
Xét phép thử: “ Chọn ngẫu nhiên 1 số từ A” ![]()
Gọi B là biến cố: “ Số được chọn chỉ có đúng 3 chữ số khác nhau”.
TH1: Có 1 chữ số được lặp lần, 2 chữ số còn lại khác nhau.
+) Chọn 1 chữ số khác 0 có 9 cách ( gọi là a).
+) Xếp 3 chữ số vào trong vị trí có cách.
+) Chọn 2 chữ số từ 8 chữ số còn lại và xếp vào 2 vị trí còn lại có cách.
![]()
TH2: Có 2 trong 5 chữ số, mỗi chữ số được lặp 2 lần.
+) Chọn 2 chữ số từ 9 chữ số có (gọi là a,b).
+) Xếp chữ số: a,a,b,b vào 4 trong 5 vị trí có cách.
+) Xếp 1 chữ số còn lại có 7 cách.
![]()
![]()
Kết luận:
![]()
Câu 8:
Gọi là tập hợp các số tự nhiên có 5 chữ số. Lấy ngẫu nhiên hai số từ tập X. Xác suất để nhận được ít nhất một số chia hết cho 4 gần nhất với số nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn A
Số phần tử không gian mẫu: ![]()
TH1: Nếu a = 2
b = 0 ![]() có 4 cách;d có 4 cách.
có 4 cách;d có 4 cách.
Vậy có 16 số.
![]() có 5 cách;c có 5 cách; d có 4 cách.
có 5 cách;c có 5 cách; d có 4 cách.
Vậy có 100 số.
TH2: Nếu ![]() có 3 cách; b có 6 cách; c có 5 cách; d có 4 cách.
có 3 cách; b có 6 cách; c có 5 cách; d có 4 cách.
Vậy có 360 số.
TH3: Nếu a = 9
b = 0; ![]() có 5 cách; d có 4 cách.
có 5 cách; d có 4 cách.
Vậy có 20 số.
Kết luận: ![]() số
số

Câu 9:
Cho một đa giác đều có 18 đỉnh nội tiếp đường tròn tâm O. Gọi X là tập hợp tất cả các tam giác có đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho. Chọn tam giác trong tập hợp X. Xác suất để tam giác được chọn là tam giác cân bằng
 Xem đáp án
Xem đáp án
Chọn B
Các số tự nhiên của tập X có dạng , suy ra tập X có 9. số. Lấy từ tập X ngẫu nhiên hai số có số.
Vì ![]()
![]() có 25 số.
có 25 số.
Suy ra số tự nhiên có năm chữ số chia hết cho 4 là 9.10.10.25 = 22500 số.
Số tự nhiên có năm chữ số không chia hết cho 4 là 9.10.10.75 = 67500 số.
Vậy xác suất để ít nhất một số chia hết cho 4 là: 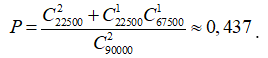
Câu 10:
Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 4 đỉnh trong các đỉnh của đa giác. Tính xác suất để 4 đỉnh lấy được tạo thành tứ giác có 2 góc ở 2 đỉnh kề chung một cạnh của tứ giác là 2 góc tù.
 Xem đáp án
Xem đáp án
Chọn D
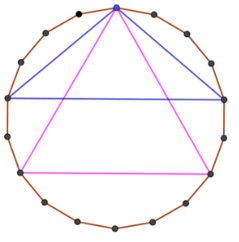
Số cách chọn 1 tam giác có 3 đỉnh trùng với 3 trong số 18 đỉnh của đa giác đã cho là ![]()
Gọi A là biến cố: “ tam giác được chọn là tam giác cân”.
- TH1: Tam giác được chọn là tam giác đều: có 6 cách.
- TH2: Tam giác được chọn là tam giác cân nhưng không phải tam giác đều:
+ Chọn đỉnh của tam giác cân có 18 cách.
+ Chọn cặp đỉnh còn lại để cùng với đỉnh đã chọn tạo thành đỉnh của tam giác cân (không đều) có 7 cách.
Suy ra số cách chọn tam giác cân nhưng không phải tam giác đều là 18.7 = 126 cách.
Vậy ![]()
![]()
