Câu hỏi:
03/04/2024 30Cho A là tập tất cả các số tự nhiên có 5 chữ số. Chọn ngẫu nhiên một số từ tập A, tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.
Trả lời:
Giải bởi Vietjack
Chọn A
Ta có tất cả các số tự nhiên có 5 chữ số bắt đầu từ 10000 đến 99999 gồm 90000 số.
Do đó = 90000
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 1.
Mà 90000 = 70x1285+50, nên ta chia 90000 số thành 1285 bộ 70 số liên tiếp và còn lại 50 số cuối, trong đó:
1285 bộ 70 số tự nhiên liên tiếp có 1285 số thỏa mãn yêu cầu
50 số cuối có 5 số tận cùng bằng 1 được xét trong bảng sau
|
99951 |
99961 |
99971 |
99981 |
99991 |
|
Chia cho 7 dư 5 |
Chia cho 7 dư 1 |
Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 3 |
Vậy tất cả có 1286 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1.
Gọi là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 1’ thì n(A) = 1286
Suy ra 
Cách 2:
Vì A là tập tất cả các số tự nhiên có 5 chữ số nên
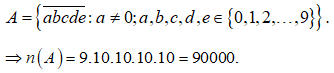
Số phần tử của không gian mẫu là 
Gọi X là biến cố: “Chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 từ tập A”.
Khi 
có tận cùng bằng 1, do đó 
với 
có chữ số tận cùng là 3.
Xét các trường hợp sau:
1) M là số có 4 chữ số có dạng Khi đó: 
- Với m = 1, do 
+) Khi n = 4 thì p > 2 nên 
. Ta được 7 số thỏa mãn.
+) Khi n5 : Có 5 cách chọn n thuộc tập hợp {5;6;7;8;9}. Khi đó p được chọn tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 50 số thỏa mãn.
- Với m2 tức là có 8 cách chọn m từ tập {2;3;4;5;6;7;8;9}. Khi đó 
với mọi n,p thuộc tập hợp {0;1;2;3;4;5;6;7;8;9}. Ta được 8.10.10 = 800 số thỏa mãn.
2) M là số có 5 chữ số có dạng Khi đó: 
Do 14285 nên m chỉ nhận giá trị bằng 1 và n 4
- Với m = 1; n = 0,1,2,3 thì p,q là các số tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 4.10.10 = 400 số thỏa mãn.
- Với m = 1; n = 4:
+) Khi p = 0 hoặc p = 1 thì q là số tùy ý thuộc tập {0;1;2;3;4;5;6;7;8;9}. Ta được 2.10 = 20 số thỏa mãn.
+) Khi p = 2 thì q phải thuộc tập {0;1;2;3;4;5;6;7;8}. Ta được 9 số thỏa mãn.
Vậy số phần tử của biến cố X là n(X) = 7 + 50 + 8000 + 429 = 1286
Xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị là 1 bằng
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Lập một số tự nhiên có 4 chữ số. Tính xác suất để số đó có chữ số đứng trước không nhỏ hơn chữ số đứng sau.
Câu 2:
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là
Câu 3:
Cho S là tập tất cả các số tự nhiên có 7 chữ số, lấy ngẫu nhiên một số từ tập S. Xác suất để số lấy được có chữ số tận cùng bằng 3 và chia hết cho 7 có kết quả gần nhất với số nào trong các số sau
Câu 4:
Trong kỳ thi Chọn học sinh giỏi tỉnh có em dự thi, có 105 em tham gia buổi gặp mặt trước kỳ thi. Biết các em đó có số thứ tự trong danh sách lập thành một cấp số cộng. Các em ngồi ngẫu nhiên vào hai dãy bàn đối diện nhau, mỗi dãy có 5 ghế và mỗi ghế chỉ ngồi được 1 học sinh. Tính xác suất để tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau.
Câu 5:
Cho tập S = {1;2;3;...;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là
Câu 6:
Cho S là tập tất cả các số tự nhiên có 7 chữ số, lấy ngẫu nhiên một số từ tập S. Xác suất để số lấy được có chữ số tận cùng bằng 3 và chia hết cho 7 có kết quả gần nhất với số nào trong các số sau
Câu 7:
Xếp ngẫu nhiên 2 quả cầu xanh, 2 quả cầu đỏ, 2 quả cầu trắng (các quả cầu này đôi một khác nhau) thành một hàng ngang. Tính xác suất để 2 quả cầu màu trắng không xếp cạnh nhau?
Câu 8:
Cho một bảng ô vuông 3x3
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng:
Câu 9:
Tung đồng thời 2 con súc sắc cân đối đồng chất. Gọi m là tích của số chấm trên hai con súc sắc trong mỗi lần tung. Tính xác suất để phương trình có hai nghiệm phân biệt.
Câu 10:
Gọi X là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau. Lấy ngẫu nhiên một số thuộc tập X. Xác suất để số lấy được luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ.
Câu 11:
Cho tập X = {1;2;3;....;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là
Câu 12:
Cho tập hợp (S). Hai bạn A, B mỗi bạn chọn ngẫu nhiên một tập con của (S). Xác suất để tập con của A và B chọn được có đúng 2 phần tử chung gần nhất với kết quả nào dưới đây?
Câu 13:
Có 3 quả cầu màu vàng, 3 quả cầu màu xanh (các quả cầu cùng màu thì giống nhau) bỏ vào hai cái hộp khác nhau, mỗi hộp quả cầu. Tính xác suất để các quả cầu cùng màu thì vào chung một hộp.
Câu 14:
Cho đa giác 30 đỉnh nội tiếp đường tròn, gọi (S) là tập hợp các đường thẳng đi qua hai trong số 30 đỉnh đã cho. Chọn 2 đường thẳng bất kỳ thuộc tập (S). Tính xác suất để chọn được 2 đường thẳng mà giao điểm của chúng nằm bên trong đường tròn.
Câu 15:
Cho một đa giác đều 48 đỉnh. Lấy ngẫu nhiên 3 đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.
