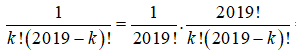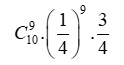299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết
299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P3)
-
737 lượt thi
-
40 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Số cách xếp 3 học sinh vào một hàng ghế dài gồm 10 ghế, mỗi ghế chỉ một học sinh ngồi bằng
 Xem đáp án
Xem đáp án
Chọn D
Chọn 3 học sinh (có thứ tự) xếp vào 10 vị trí có số cách chọn là số chỉnh hợp chập 3 của 10 phần tử:
Câu 2:
Tổ 1 gồm 10 bạn học sinh. Có bao nhiêu cách để cô giáo chủ nhiệm chọn ra 4 em đi bưng bàn ghế?
 Xem đáp án
Xem đáp án
Chọn A
Chọn 4 học sinh trong 10 học sinh tổ 1 để đi bưng bàn ghế ta có cách.
Câu 3:
Từ các chữ số 1,2,3,....,9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau
 Xem đáp án
Xem đáp án
Chọn B
Gọi số cần tìm có dạng là ![]()
Mỗi bộ ba số ![]() là một chỉnh hợp chập 3 của 9 phần tử.
là một chỉnh hợp chập 3 của 9 phần tử.
Vậy số các số cần tìm là số.
Câu 4:
Trong mặt phẳng, cho tập S gồm 10 điểm, trong đó không có 3 điểm nào thẳng hàng. Có bao nhiêu tam giác có 3 đỉnh đều thuộc ?
 Xem đáp án
Xem đáp án
Chọn B
Số tam giác có 3 đỉnh thuộc S bằng số tổ hợp chập 3 của 10: = 120
Câu 5:
Một tập hợp M có tập con. Hỏi M có bao nhiêu tập con có ít nhất 2017 phần tử?
 Xem đáp án
Xem đáp án
Chọn A
Công thức tính số tập con của một tập hợp gồm n phần tử là
Tập M có tập con nên có 2018 phần tử.
Số tập con có 2017 phần tử là 2018(tập con).
Số tập con có 2018 phần tử là = 2018 (tập con).
Số tập con có ít nhất 2017 phần tử của M là (tập con).
Câu 6:
Một lớp học gồm có 20 học sinh nam và 15 học sinh nữ. Cần chọn ra 2 học sinh, 1 nam và 1 nữ để phân công trực nhật. Số cách chọn là
 Xem đáp án
Xem đáp án
Chọn A
Chọn 1 nam trong 20 học sinh nam có cách.
Chọn 1 nữ trong 15 học sinh nữ có cách.
Áp dụng quy tắc nhân có : . = 300 cách.
Câu 7:
Cho k, n là số nguyên dương thỏa mãn 1k n. Đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn D
Theo tính chất tổ hợp SGK:
Câu 8:
Cho đa giác đều có 20 cạnh. Có bao nhiêu hình chữ nhật (không phải là hình vuông), có các đỉnh là đỉnh của đa giác đều đã cho?
 Xem đáp án
Xem đáp án
Chọn C
Đa giác đều có 20 cạnh thì sẽ có tất cả 10 đường chéo đi qua tâm của đa giác.
Một hình chữ nhật được tạo thành từ 2 đường chéo đi qua tâm, suy ra số hình chữ nhật được tạo thành là
Hình vuông được tạo thành từ 2 đường chéo vuông góc nhau, ta có tất cả 5 cặp đường chéo vuông góc nhau, suy ra có tất cả 5 hình vuông.
Vậy có 40 hình chữ nhật (không phải hình vuông) được tạo thành.
Câu 9:
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?
 Xem đáp án
Xem đáp án
Chọn C.
Gọi số cần tìm là n = .
Ta có a có 9 cách chọn. Số cách xếp các số còn lại vào vị trí b, c là .
Vậy số các số cần tìm là 9. = 648.
Câu 10:
Cho các số nguyên dương tùy ý k, n thỏa mãn kn. Đẳng thức nào dưới đây đúng ?
 Xem đáp án
Xem đáp án
Chọn D
Dựa vào công thức ta có
Câu 11:
Cho A = {1,2,3,4}. Từ A lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau?
 Xem đáp án
Xem đáp án
Chọn B
Mỗi số tự nhiên có 4 chữ số đôi một khác nhau được lập bằng cách lấy các phần tử của tập hợp A và sắp xếp theo một thứ tự nhất định là một hoán vị của 4 phần tử.
Vậy có tất cả 4! = 24 số tự nhiên có 4 chữ số đôi một khác nhau được lập từ ![]() .
.
Câu 12:
Trong kho đèn trang trí đang có 5bóng đèn loại I, 7 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 5 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II.
 Xem đáp án
Xem đáp án
Chọn A
+ Gọi x là số bóng đèn loại I được lấy ra, y là số bóng đèn loại II được lấy ra, x,y .
+ Suy ra 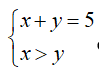 có các trường hợp
có các trường hợp ![]()
+ Số khả năng xảy ra là ![]() .
.
Câu 13:
Gieo 2 xúc xắc màu xanh và đỏ cùng 1 lần. Hỏi có bao nhiêu khả năng xảy ra số chấm xuất hiện của xúc xắc màu xanh nhiều hơn số chấm xuất hiện trên xúc xắc màu đỏ.
 Xem đáp án
Xem đáp án
Chọn B
+ Không gian mẫu là 6*6 = 36.
+ Vì gieo 2 con xúc xắc 1 lần nên có 3 trường hợp về số chấm xuất hiện như sau.
Trường hợp 1: Số chấm trên con màu xanh lớn hơn số chấm trên con màu đỏ.
Trường hợp 2: Số chấm trên con màu đỏ lớn hơn số chấm trên con màu xanh.
Trường hợp 3: Số chấm trên con màu xanh bằng số chấm trên con màu đỏ, có 6 khả năng.
Trong đó trường hợp 1 và 2 bằng về số lượng xuất hiện.
+ Nên trường hợp số chấm trên con màu xanh nhiều hơn số chấm trên con màu đỏ có (36-6)/2 = 15 khả năng.
Câu 14:
Từ các chữ số 1,2,3,4,5,6 lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau?
 Xem đáp án
Xem đáp án
Chọn C
Mỗi số tự nhiên có 3 chữ số khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6 là một chỉnh hợp chập 3 của 6 và ngược lại. Vậy có số tự nhiên thỏa mãn yêu cầu bài toán.
Câu 15:
Có tất cả 120 cách chọn 3 học sinh từ nhóm n(chưa biết) học sinh. Số n là nghiệm của phương trình nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
Số cách chọn 3 trong n học sinh có 
Khi đó ![]()
Câu 16:
Cho n là số nguyên dương và = 792. Tính .
 Xem đáp án
Xem đáp án
Chọn B
Điều kiện ![]()
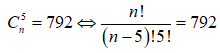
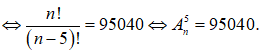
Cách 2: ( FB: Hồng Minh Trần). Áp dụng công thức ![]() ta có:
ta có:
![]()
Câu 17:
Có 6 học sinh và 3thầy giáo A, B, C ngồi trên một hàng ngang có 9 ghế. Số cách xếp chỗ ngồi cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là
 Xem đáp án
Xem đáp án
Chọn A
Xếp 6 học sinh có 6! cách xếp.
Giữa 6 học sinh có 5 khoảng trống.
Xếp 3 thầy giáo A, B, C vào 5 khoảng trống trên có: cách.
Vậy số cách xếp thỏa mãn yêu cầu là: 6!. = 43200 cách.
Câu 18:
Số cách chọn 3 người từ một nhóm có 12 người là
 Xem đáp án
Xem đáp án
Chọn C
Số cách chọn 3 người từ một nhóm 12 người là:
Câu 19:
Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau, sao cho trong mỗi số đó nhất thiết phải có mặt chữ số 0?
 Xem đáp án
Xem đáp án
Chọn B
Gọi số cần tìm là : ![]() chẵn và trong số luôn có mặt số 0.
chẵn và trong số luôn có mặt số 0.
Số cần tìm được chọn từ một trong các trường hợp :
Trường hợp 1 : = 0 có 5 cách chọn.
Khi đó ![]() cách chọn. Suy ra có : (số).
cách chọn. Suy ra có : (số).
Trường hợp 2 : ![]() có 4 cách chọn.
có 4 cách chọn.
Chữ số 0 có 3 cách chọn vị trí ![]() cách chọn 3 số cho 3 vị trí còn lại.
cách chọn 3 số cho 3 vị trí còn lại.
Suy ra có : 4.3. (số).
Vậy ta có ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Câu 20:
Từ một tập gồm 10 câu hỏi trong đó có 4 câu lý thuyết và 6 câu bài tập, người ta tạo thành các đề thi. Biết rằng một đề thi phải gồm 3 câu hỏi trong đó có ít nhất một câu lý thuyết và một câu bài tập. Hỏi có thể tạo bao nhiêu đề khác nhau ?
 Xem đáp án
Xem đáp án
Chọn A
Xảy ra hai trường hợp
TH1 : 2 câu lý thuyết, 1 câu bài tập có ![]() .
.
TH2 : 1 câu lý thuyết, 2 câu bài tập có ![]() .
.
Vậy có thể tạo 60 + 36 = 96A. 96 đề khác nhau.
Câu 21:
Số tập con gồm nhiều nhất 3 phần tử của tập A = {1,2,....,10} là
 Xem đáp án
Xem đáp án
Chọn D
Số tập con có k phần tử của tập A là .
=> Số tập con gồm nhiều nhất 3 phần tử của tập A là
Câu 22:
Có bao nhiêu số tự nhiên có ba chữ số đôi một khác nhau.
 Xem đáp án
Xem đáp án
Chọn D
Cách 1:
Gọi số cần tìm là: ![]()
Khi đó:

Theo quy tắc nhân có 9.9.8 = 648 số thỏa mãn yêu cầu bài toán.
Cách 2:
Gọi số cần tìm là ![]()
Khi đó:
![]()
Chọn b,c từ 9 số còn lại là một chỉnh hợp chập 2 của 9 phần tử, số cách chọn cách.
Số các số cần tìm : 9. = 648 số
Câu 23:
Có bao nhiêu cách bỏ đồng thời 7 quả bóng bàn giống nhau vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả?
 Xem đáp án
Xem đáp án
Chọn B
Đặt 7 quả bóng trên bàn, giữa 7 quả bóng có 6 khoảng trống. Ta muốn chia làm 4 phần thì ta dùng 3cái que, ta đặt vào 3 trong 6 khoảng trống, ta có cách đt.
Do đó số cách chia 7 quả bóng thành 4 phần để bỏ vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả là: = 20 cách
Câu 25:
Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, AD lần lượt lấy 3;4;5;6 điểm phân biệt khác các điểm A, B, C, D. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
 Xem đáp án
Xem đáp án
Chọn A
Tổng số điểm vừa lấy bằng: 3 + 4 + 5 + 6 = 18 (điểm).
Mỗi cách chọn ra 3 điểm không nằm trên một cạnh cho ta một tam giác.
Số cách chọn 3 điểm từ 18 điểm là: = 816(cách chọn).
Số cách chọn 3 điểm cùng nằm trên một cạnh là: ![]() (cách chọn).
(cách chọn).
Vậy số tam giác cần tìm bằng: 816 - 35 = 781(tam giác).
Câu 26:
Đội văn nghệ của trường THPT Hùng Vương có 9 học sinh, trong đó có 4 học sinh lớp 12, 3 học sinh lớp 11 và 2 học sinh lớp 10. Hỏi có bao nhiêu cách chọn ra một nhóm có ít nhất 3 học sinh để biểu diễn dịp 26 tháng 3 sao cho mỗi khối có ít nhất một học sinh, biết rằng năng khiếu văn nghệ của các em là như nhau
 Xem đáp án
Xem đáp án
Chọn B
TH1: Nhóm có đúng 3 học sinh có ![]() cách chọn
cách chọn
TH2: Nhóm có đúng 4 học sinh có ![]() cách chọn
cách chọn
TH3: Nhóm có đúng 5 học sinh có ![]() cách chọn
cách chọn
TH4: Nhóm có đúng 6 học sinh có ![]() cách chọn
cách chọn
TH5: Nhóm có đúng 7 học sinh có ![]() cách chọn
cách chọn
TH6: Nhóm có đúng 8 học sinh có ![]() cách chọn
cách chọn
TH7: Nhóm có đúng 9 học sinh có ![]() cách chọn
cách chọn
Vậy tổng số có 24 + 72 + 98 + 76 + 35 + 9 + 1 = 315 cách.
Câu 27:
Có bao nhiêu số tự nhiên có hai chữ số, các chữ số khác nhau và đều khác không?
 Xem đáp án
Xem đáp án
Chọn B
Từ các chữ số trong tập {1;2;3;4;5;6;7;8;9} lập được số tự nhiên có hai chữ số khác nhau và đều khác 0
Câu 28:
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247
 Xem đáp án
Xem đáp án
Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành là:
![]()
Câu 29:
Cho tam giác ABC, gọi S là tập hợp gồm 4 đường thẳng song song với AB, 6 đường thẳng song song với BC và 8 đường thẳng song song với AC. Hỏi có bao nhiêu hình bình hành được tạo thành từ các đường thẳng thuộc tập ![]()
 Xem đáp án
Xem đáp án
Chọn B
Ta chia tập Sthành 3 nhóm, nhóm 1 gồm 4 đường thẳng song song với AB, nhóm 2 gồm 6 đường thẳng song song với BC, nhóm 3 gồm 8 đường thẳng song song với AC. Khi đó cứ 2 đường thẳng thuộc nhóm này và hai đường thẳng thuộc nhóm khác sẽ tạo thành một hình bình hành. Khi đó số hình bình hành là:
![]()
Câu 30:
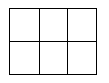
Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng hai cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?
 Xem đáp án
Xem đáp án
Chọn D
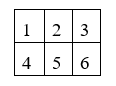
+ Tô màu ô vuông số 2: có cách chọn 2 trong 3 màu, có cách tô 2 màu đó lên 4 cạnh. Vậy có = 18cách.
+ Tô màu ô vuông số 1,5,3: có cách chọn màu còn lại, có cách tô màu còn lại lên 3 cạnh còn lại của 1 hình vuông. Vậy có ( = cách
+ Tô màu ô vuông số 4,6: Mỗi 1 hình vuông có 2 cách tô màu. Vậy có = 4cách.
Vậy có 18..4 = 15552 cách thỏa mãn.
Câu 31:
Có bao nhiêu cách chia hết 4 chiếc bánh khác nhau cho 3 em nhỏ, biết rằng mỗi em nhận được ít nhất 1 chiếc.
 Xem đáp án
Xem đáp án
Chọn C
Chia 4 chiếc bánh khác nhau cho 3 em nhỏ, biết rằng mỗi em nhận được ít nhất 1 chiếc nên sẽ có một em nhận được ![]() chiếc, hai em còn lại mỗi em nhận được 2 chiếc.
chiếc, hai em còn lại mỗi em nhận được 2 chiếc.
Chọn 2 trong 4 chiếc bánh chia cho 1 trong 3 em có .3 cách.
Lấy 2 chiếc bánh còn lại chia cho hai em còn lại có 2! cách.
Vậy .3.2! = 36 cách.
Câu 32:
Cho tập hợp A có 3 phần tử, số hoán vị các phần tử của A bằng
 Xem đáp án
Xem đáp án
Chọn C
Số các hoán vị gồm 3 phần tử của A là = 3! = 6
Câu 33:
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n, mệnh đề nào dưới đây sai??
 Xem đáp án
Xem đáp án
Chọn D
Câu 34:
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n, mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Chọn C
Câu 35:
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n, mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Chọn B
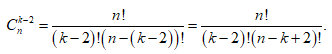
Câu 36:
Cho k, n(k < n) là các số nguyên dương, mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Chọn C
Ta có  nên A đúng.
nên A đúng.
Vì ![]() nên B đúng
nên B đúng
Ta có 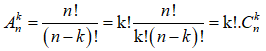 nên D đúng và C sai.
nên D đúng và C sai.
Câu 37:
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n-1, mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Chọn A
Vì ![]()
![]() là mệnh đề sai
là mệnh đề sai
Câu 38:
Từ các chữ số thuộc tập hợp S = {1;2;3;4;5;6;7;8;9} có bao nhiêu số có 9 chữ số khác nhau sao cho chữ số 1 đứng trước chữ số 2, chữ số 3 đứng trước chữ số 4, chữ số 5 đứng trước chữ số 6 ?
 Xem đáp án
Xem đáp án
Chọn C
Xếp chữ số 1 và 2 vào hai vị trí, do không giao hoán nên có: (cách).
Tương tự xếp chữ số 3 và 4 có (cách), xếp chữ số 5 và 6 có (cách).
Ba chữ số 7,8,9 hoán vị vào ba vị trí còn lại, có số cách xếp là 3! (cách).
Vậy số các chữ số thỏa mãn bài toán là: .3! = 45360(số).
Câu 39:
Từ các chữ số {0;1;2;3;4} lập được tất cả bao nhiêu số chẵn có 4 chữ số khác nhau sao cho chữ số 2 và 3 đứng cạnh nhau.
 Xem đáp án
Xem đáp án
Chọn D
Gọi số cần tìm có dạng ![]() là các số thuộc tập hợp {0;1;2;3;4}
là các số thuộc tập hợp {0;1;2;3;4}
Vì chữ số 2 và 3 đứng cạnh nhau và số lập được là chẵn nên ta có các trường hợp như sau:
TH1: Số có dạng ![]()
+ Chọn d có 2 cách.
+ Chọn c có 2 cách.
Vậy có 2.2.2 = 8 kết quả của TH1.
TH2: Số có dạng ![]()
* Nếu d = 0 thì chọn a có 2 cách.
* Nếu d = 4 thì chọn a có 1 cách.
Vậy có 2.(1+2) = 6 kết quả của TH2.
TH5: Số có dạng ![]()
+ Chọn a có 2 cách.
+ Chọn b có 2 cách.
Vậy có 2.2 = 4 kết quả của TH5.
Vậy có tất cả 8 + 6 + 4 = 18 kết quả thỏa mãn.
Câu 40:
Đề kiểm tra 15 phút có 10 câu trắc nghiệm, mỗi câu có bốn phương án trả lời, trong đó có một phương án đúng, mỗi câu trả lời đúng được 1,0 điểm. Một thí sinh làm cả 10 câu, mỗi câu chọn một phương án. Tính xác suất để thí sinh đó đạt từ 8,0 điểm trở lên.
 Xem đáp án
Xem đáp án
Chọn A
Cách 1: Vì mỗi câu hỏi có bốn phương án trả lời và chỉ có một phương án đúng nên xác suất để trả lời đúng và xác suất để trả lời sai một câu hỏi lần lượt là
Theo yêu cầu của bài toán có các trường hợp sau:
|
Trường hợp |
Số câu trả lời đúng |
Số câu trả lời sai |
Xác suất xảy ra |
|
TH1 |
8 |
2 |
(quy tắc nhân) |
|
TH2 |
9 |
1 |
(quy tắc nhân) |
|
TH3 |
10 |
0 |
(quy tắc nhân) |
Vậy áp dụng quy tắc cộng ta có xác suất cần tìm là:
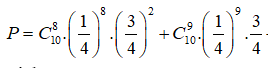
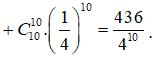
Cách 2:
- Số cách làm bài của thí sinh: (cách).
- Để thí sinh đó đạt từ 8,0 điểm trở lên, ta có 3 trường hợp sau:
+ Làm được 8 câu đúng và 2 câu sai (8 điểm): ![]()
+ Làm được 9 câu đúng và 1 câu sai (9 điểm): ![]()
+ Làm được 10 câu đúng (10 điểm): 1 (cách).
Do đó số cách để thí sinh đạt từ 8,0 điểm trở lên là: ![]()
Vậy xác suất cần tìm là ![]()