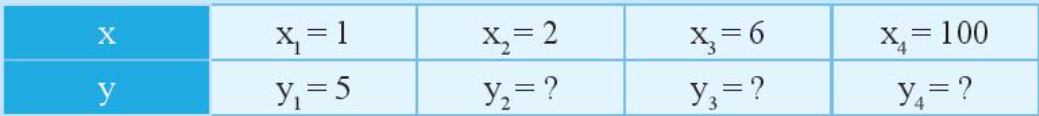Giải SGK Toán 7 Bài 2 (Chân trời sáng tạo): Đại lượng tỉ lệ thuận

Giải SGK Toán 7 Bài 2: Đại lượng tỉ lệ thuận

Giải Toán 7 trang 11 Tập 2

Khởi động trang 11 Toán 7 Tập 2 :

Cho biết dây điện có giá 10 nghìn đồng một mét. Gọi y (nghìn đồng) là giá tiền của x (mét) dây điện. Hãy tính y theo x.

Lời giải:

Theo đề bài, dây điện có 10 nghìn đồng một mét.

Do đó giá tiền của x mét là 10x nghìn đồng.

Khám phá 1 trang 11 Toán 7 Tập 2 :

a) Học sinh trường Nguyễn Huệ tham gia phong trào “Trồng cây xanh bảo vệ môi trường”, mỗi em đều trồng được 4 cây. Gọi c là số cây trồng được, h là số học sinh đã tham gia. Em hãy viết công thức tính c theo h.

b) Tìm điểm giống nhau giữa hai công thức y = 10x và c = 4h.

Lời giải:

a) Theo đề bài, mỗi em trồng được 4 cây, có h em học sinh tham gia.

Do đó số cây trồng được là 4h cây.

Vậy công thức tính c theo h là c = 4h.

b) Công thức y = 10x có đại lượng y gấp 10 lần đại lượng x.

Công thức c = 4h có đại lượng c gấp 4 lần đại lượng h.

Vậy điểm giống nhau giữa hai công thức này là có một đại lượng gấp k lần đại lượng còn lại (k ≠ 0).

Thực hành 1 trang 11 Toán 7 Tập 2 :

a) Cho hai đại lượng f và x liên hệ với nhau theo công thức f = 5x. Hãy cho biết đại lượng x có tỉ lệ thuận với đại lượng f hay không. Hệ số tỉ lệ là bao nhiêu?

b) Cho đại lượng P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g = 9,8. Hãy viết công thức tính P theo m.

Lời giải:

a) Ta có f = 5x suy ra x = $\frac{f}{5}$ = $\frac{1}{5}$f.

Do đó đại lượng x tỉ lệ thuận với đại lượng f với hệ số tỉ lệ là $\frac{1}{5}$.

b) Do đại lượng P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g = 9,8 nên P = 9,8 . m.

Vậy công thức tính P theo m là P = 9,8 . m.

Vận dụng 1 trang 11 Toán 7 Tập 2:

Cho biết khối lượng mỗi mét khối của một số kim loại như sau:

đồng: 8 900 kg; vàng: 19 300 kg; bạc: 10 500 kg.

Hãy viết công thức tính khối lượng m (kg) theo thể tích V (m³) của mỗi kim loại và cho biết m tỉ lệ thuận với V theo hệ số tỉ lệ là bao nhiêu.

Lời giải:

Theo đề bài, m tỉ lệ thuận với V nên:

• Mỗi m³ đồng có khối lượng 8 900 kg nên công thức tính khối lượng m (kg) theo thể tích V (m³) là m = 8 900V.
• Mỗi m³ vàng có khối lượng 19 300 kg nên công thức tính khối lượng m (kg) theo thể tích V (m³) là m = 19 300V.
• Mỗi m³ đồng có khối lượng 10 500 kg nên công thức tính khối lượng m (kg) theo thể tích V (m³) là m = 10 500V.

Giải Toán 7 trang 12 Tập 2

Khám phá 2 trang 12 Toán 7 Tập 2 :

Cho biết giá trị tương ứng của hai đại lượng y và x tỉ lệ thuận với nhau trong bảng sau:

a) Hãy xác định hệ số tỉ lệ của y đối với x.

b) Tính các giá trị tương ứng chưa biết của y.

c) So sánh các tỉ số giữa hai giá trị tương ứng của y và x.

$\frac{y_1}{x_1}$, $\frac{y_2}{x_2}$, $\frac{y_3}{x_3}$, $\frac{y_4}{x_4}$.

Lời giải:

a) Ta có: x₁ = 1; y₁ = 5 suy ra y₁ = 5x₁.

Vì đại lượng y tỉ lệ thuận với đại lượng x và y₁ = 5x₁ nên hệ số tỉ lệ của y đối với x là 5.

b) Ta có hệ số tỉ lệ của y đối với x là 5 nên:

Với x₂ = 2 thì y₂ = 5.2 = 10.

Với x₃ = 6 thì y₃ = 5.6 = 30.

Với x₄ = 100 thì y₄ = 5.100 = 500.

c) Ta có $\frac{y_1}{x_1}=\frac{5}{1}=5$; $\frac{y_2}{x_2}=\frac{10}{2}=5$; $\frac{y_3}{x_3}=\frac{30}{6}=5$; $\frac{y_4}{x_4}=\frac{500}{100}=5$.

Thực hành 2 trang 12 Toán 7 Tập 2 :

Trong các trường hợp sau, hãy kiểm tra xem hai đại lượng m và n có tỉ lệ thuận với nhau hay không.

a) 

b)

Lời giải:

a) Với m = 2, n = 4 thì $\frac{m}{n}=\frac{2}{4}=\frac{1}{2}$.

Với m = 4, n = 16 thì $\frac{m}{n}=\frac{4}{16}=\frac{1}{4}$.

Do $\frac{1}{2}\ne \frac{1}{4}$ nên m và n không phải hai đại lượng tỉ lệ thuận.

b) Với m = 1, n = -5 thì $\frac{m}{n}=\frac{1}{-5}$.

Với m = 2, n = -10 thì $\frac{m}{n}=\frac{2}{-10}=\frac{1}{-5}$.

Với m = 3, n = -15 thì $\frac{m}{n}=\frac{3}{-15}=\frac{1}{-5}$.

Với m = 4, n = -20 thì $\frac{m}{n}=\frac{4}{-20}=\frac{1}{-5}$.

Với m = 5, n = -25 thì $\frac{m}{n}=\frac{5}{-25}=\frac{1}{-5}$.

Do đó m và n là hai đại lượng tỉ lệ thuận.

Giải Toán 7 trang 13 Tập 2

Vận dụng 2 trang 13 Toán 7 Tập 2 :

Cho biết hai đại lượng m và n tỉ lệ thuận với nhau. Hãy tìm giá trị của a và b.

Lời giải:

a) Do m và n là hai đại lượng tỉ lệ thuận với nhau và với m = 2 thì n = -6, với m = 3 thì

n = -9.

Ta thấy -6 = (-3) . 2, -9 = (-3) . 3.

Do đó hệ số tỉ lệ của n đối với m là -3.

Khi đó với m = 4 thì n = (-3) . 4 = -12.

Với n = -18 thì m = (-18) : (-3) = 6.

Vậy a = -12, b = 6.

Giải Toán 7 trang 14 Tập 2

Vận dụng 3 trang 14 Toán 7 Tập 2 :

Hai lớp 7A và 7B quyên góp được một số sách tỉ lệ thuận với số học sinh của lớp, biết số học sinh của hai lớp lần lượt là 32 và 36. Lớp 7A quyên góp được ít hơn lớp 7B 8 quyển sách. Hỏi mỗi lớp quyên góp được bao nhiêu quyển sách?

Lời giải:

Gọi a (quyển sách) và b (quyển sách) lần lượt là số sách hai lớp 7A và 7B quyên góp được

(a, b $\in$ℕ*).

Vì số học sinh của hai lớp lần lượt là 32 và 36 nên $\frac{a}{32}=\frac{b}{36}$ hay $\frac{a}{8}=\frac{b}{9}$.

Vì số sách quyên góp được tỉ lệ thuận với số học sinh của lớp nên $\frac{a}{8}=\frac{b}{9}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{a}{8}=\frac{b}{9}=\frac{b-a}{9-8}=\frac{8}{1}=8$.

Khi đó a = 8.8 = 64, b = 9.8 = 72 (thỏa mãn).

Vậy số sách quyên góp được của hai lớp 7A và 7B lần lượt là 64 quyển và 72 quyển.

Bài 1 trang 14 Toán 7 Tập 2 :

Cho hai đại lượng a và b tỉ lệ thuận với nhau. Biết khi a = 2 thì b = 18.

a) Tìm hệ số tỉ lệ k của a đối với b.

b) Tính giá trị của b khi a = 5.

Lời giải:

a) Khi a = 2 thì b = 18 thì $\frac{a}{b}=\frac{2}{18}=\frac{1}{9}$.

Ta có a và b là hai đại lượng tỉ lệ thuận với nhau và $\frac{a}{b}=\frac{1}{9}$.

Do đó hệ số tỉ lệ k của a đối với b là $\frac{1}{9}$.

b) Khi a = 5 thì b = a : $\frac{1}{9}$ = 5 : $\frac{1}{9}$ = 5.9 = 45.

Vậy b = 45 khi a = 5.

Bài 2 trang 14 Toán 7 Tập 2 :

Cho hai đại lượng x và y tỉ lệ thuận với nhau. Biết rằng khi x = 7 thì y = 21.

a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.

b) Tìm hệ số tỉ lệ của x đối với y và biểu diễn x theo y.

Lời giải:

a) Khi x = 7 thì y = 21 thì $\frac{y}{x}=\frac{21}{7}=3$.

Ta có x và y là hai đại lượng tỉ lệ thuận với nhau và $\frac{y}{x}=3$.

Do đó hệ số tỉ lệ của y đối với x là 3 và y = 3x.

b) Khi x = 7 thì y = 21 thì $\frac{x}{y}=\frac{7}{21}=\frac{1}{3}$.

Ta có x và y là hai đại lượng tỉ lệ thuận với nhau và $\frac{x}{y}=\frac{1}{3}$.

Do đó hệ số tỉ lệ của x đối với y là $\frac{1}{3}$ và x = $\frac{1}{3}$y.

Bài 3 trang 14 Toán 7 Tập 2 :

Cho m và n là hai đại lượng tỉ lệ thuận với nhau. Hãy viết công thức tính m theo n và tính các giá trị chưa biết trong bảng sau:

Lời giải:

Do m và n là hai đại lượng tỉ lệ thuận với nhau và với n = 1 thì m = -5.

Khi đó $\frac{m}{n}=\frac{-5}{1}=-5$.

Do đó công thức tính m theo n là m = -5n.

∙ Với n = -2 thì m = (-5) . (-2) = 10.

∙ Với n = -1 thì m = (-5) . (-1) = 5.

∙ Với n = 0 thì m = (-5) . 0 = 0.

∙ Với n = 2 thì m = (-5) . 2 = -10.

Từ đó ta có bảng sau:

Bài 4 trang 14 Toán 7 Tập 2 :

Cho biết hai đại lượng S và t tỉ lệ thuận với nhau:

a) Tính các giá trị chưa biết trong bảng trên.

b) Viết công thức tính t theo S.

Lời giải:

a) Ta có S và t là hai đại lượng tỉ lệ thuận với nhau và với S = 1 thì t = -3.

Khi đó $\frac{t}{S}=\frac{-3}{1}=-3$ hay t = -3S.

∙ Với S = 2 thì t = (-3).2 = -6.

∙ Với S = 3 thì t = (-3).3 = -9.

∙ Với S = 4 thì t = (-3).4 = -12.

∙ Với S = 5 thì t = (-3).5 = -15.

Từ đó ta có bảng sau:

b) Từ câu a ta có công thức tính t theo S là: t = -3S.

Bài 5 trang 14 Toán 7 Tập 2 :

Trong các trường hợp sau, hãy kiểm tra xem đại lượng x có tỉ lệ thuận với đại lượng y hay không.

a)

b)

Lời giải:

a) Dựa vào bảng trên, ta có:

∙ Với x = 2, y = 1,2 thì $\frac{x}{y}=\frac{2}{\mathrm{1,2}}=\frac{5}{3}$.

∙ Với x = 4, y = 2,4 thì $\frac{x}{y}=\frac{4}{\mathrm{2,4}}=\frac{5}{3}$.

∙ Với x = 6, y = 3,6 thì $\frac{x}{y}=\frac{6}{\mathrm{3,6}}=\frac{5}{3}$.

∙ Với x = -8, y = -4,8 thì $\frac{x}{y}=\frac{-8}{-\mathrm{4,8}}=\frac{5}{3}$.

Do đó $\frac{2}{\mathrm{1,2}}=\frac{4}{\mathrm{2,4}}=\frac{6}{\mathrm{3,6}}=\frac{-8}{-\mathrm{4,8}}$ nên x và y là hai đại lượng tỉ lệ thuận với nhau.

Vậy đại lượng x tỉ lệ thuận với đại lượng y.

b) Dựa vào bảng trên, ta có:

Với x = 1, y = 3 thì $\frac{x}{y}=\frac{1}{3}$.

Với x = 5, y = 25 thì $\frac{x}{y}=\frac{5}{25}=\frac{1}{5}$.

Do $\frac{1}{3}\ne \frac{1}{5}$ nên x và y không phải hai đại lượng tỉ lệ thuận.

Vậy đại lượng x không tỉ lệ thuận với đại lượng y.

Giải Toán 7 trang 15 Tập 2

Bài 6 trang 15 Toán 7 Tập 2 :

Hai chiếc nhẫn bằng kim loại đồng chất có thể tích là 3 cm³ và 2 cm³. Hỏi mỗi chiếc nặng bao nhiêu gam, biết rằng hai chiếc nhẫn nặng 96,5 g? (Cho biết khối lượng và thể tích là hai đại lượng tỉ lệ thuận với nhau).

Lời giải:

Gọi x (g) và y (g) lần lượt là khối lượng của hai chiếc nhẫn có thể tích là 3 cm³ và 2 cm³ (0 < x, y < 96,5).

Hai chiếc nhẫn nặng 96,5 g nên ta có: x + y = 96,5

Vì khối lượng và thể tích là hai đại lượng tỉ lệ thuận với nhau nên ta có $\frac{x}{3}=\frac{y}{2}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{x}{3}=\frac{y}{2}=\frac{x+y}{3+2}=\frac{\mathrm{96,5}}{5}=\mathrm{19,3}$.

Suy ra x = 3.19,3 = 57,9; y = 2.19,3 = 38,6 (thỏa mãn).

Vậy khối lượng hai chiếc nhẫn là 57,9 g và 38,6 g.

Bài 7 trang 15 Toán 7 Tập 2 :

Bốn cuộn dây diện cùng loại có tổng khối lượng là 26 kg.

a) Tính khối lượng từng cuộn, biết cuộn thứ nhất nặng bằng $\frac{1}{2}$ cuộn thứ hai, bằng $\frac{1}{4}$ cuộn thứ ba và bằng $\frac{1}{6}$ cuộn thứ tư.

b) Biết cuộn thứ nhất dài 100 m, hãy tính xem một mét dây điện nặng bao nhiêu gam.

Lời giải:

a) Gọi a, b, c, d lần lượt là khối lượng của 4 cuộn dây điện thứ nhất, thứ hai, thứ ba và thứ tư (a, b, c, d > 0).

Theo đề bài, bốn cuộn dây diện có tổng khối lượng là 26 kg nên a + b + c + d = 26.

Vì tỉ số giữa khối lượng của các cuộn dây nên:

a : b : c : d = 1 : 2 : 4 : 6 hay $\frac{a}{1}=\frac{b}{2}=\frac{c}{4}=\frac{d}{6}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{a}{1}=\frac{b}{2}=\frac{c}{4}=\frac{d}{6}=\frac{a+b+c+d}{1+2+4+6}=\frac{26}{13}=2$

Suy ra a = 1.2 = 2, b = 2.2 = 4, c = 4.2 = 8, d = 6.2 = 12 (thỏa mãn).

Vậy khối lượng của 4 cuộn dây lần lượt là 2 kg, 4 kg, 8 kg, 12 kg.

b) Đổi 2 kg = 2 000 g.

Khi đó một mét dây nặng là:

2 000 : 100 = 20 (g).

Vậy một mét dây nặng 20 g.

Bài 8 trang 15 Toán 7 Tập 2 :

Một tam giác có độ dài ba cạnh tỉ lệ với 3; 4; 5 và có chu vi là 60 cm. Tính độ dài các cạnh của tam giác đó.

Lời giải:

Gọi a, b, c (cm) lần lượt là độ dài ba cạnh của tam giác (0 < a, b, c < 60).

Theo đề bài, chu vi tam giác là 60 cm nên: a + b + c = 60

Vì độ dài ba cạnh tỉ lệ với 3; 4; 5 nên $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5$.

Suy ra x = 3.5 = 15, y = 4.5 = 20, z = 5.5 = 25 (thỏa mãn).

Vậy độ dài ba cạnh của tam giác lần lượt là 15 cm, 20 cm và 25 cm.

Bài 9 trang 15 Toán 7 Tập 2 :

Tiến, Hùng và Mạnh cùng đi câu cá trong dịp hè. Tiến câu được 12 con, Hùng câu được 8 con và Mạnh câu được 10 con. Số tiền bán cá thu được tổng cộng là 180 nghìn đồng. Hỏi nếu đem số tiền trên chia cho các bạn theo tỉ lệ với số con cá từng người câu được thì mỗi bạn nhận được bao nhiêu tiền?

Lời giải:

Gọi x, y, z (nghìn đồng) lần lượt là số tiền Tiến, Hùng và Mạnh nhận được (0 < x, y, z < 180).

Theo đề bài, số tiền bán cá thu được tổng cộng là 180 nghìn đồng nên ta có:

x + y + z = 180

Vì số tiền được nhận tỉ lệ với số cá từng người câu được nên $\frac{x}{12}=\frac{y}{8}=\frac{z}{10}$.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{12}=\frac{y}{8}=\frac{z}{10}=\frac{x+y+z}{12+8+10}=\frac{180}{30}=6$

Suy ra x = 6 . 12 = 72, y = 6 . 8 = 48, z = 6 . 10 = 60 (thỏa mãn).

Vậy số tiền Tiến, Hùng và Mạnh nhận được lần lượt là 72 nghìn đồng, 48 nghìn đồng và 60 nghìn đồng.

Xem thêm lời giải bài tập SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau

Bài 3: Đại lượng tỉ lệ nghịch

Bài 4: Hoạt động thực hành và trải nghiệm. Các đại lượng tỉ lệ trong thực tế

Bài tập cuối chương 6

Bài 1: Biểu thức số, biểu thức đại số