Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt

Bài 10 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD. Tính khoảng cách giữa AM và NP.

Trả lời

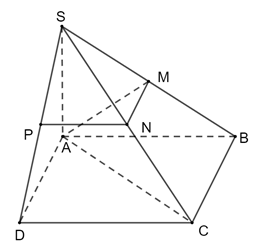
Vì SA ⊥ (ABCD) nên SA ⊥ BC

Mà BC ⊥ AB nên BC ⊥ (SAB)

Tam giác SBC có:

M là trung điểm SB

N là trung điểm SC

Do đó MN là đường trung bình nên MN // BC, $\mathrm{MN}=\frac{1}{2}\mathrm{BC}=\frac{a}{2}$ .

Mà BC ⊥ (SAB) ⇒ MN ⊥ (SAB) ⇒ MN ⊥ AM.

Tam giác SCD cóN là trung điểm SC; P là trung điểm SD

Suy ra P là đường trung bình nên NP // CD.

Mà MN // BC, BC ⊥ CD nên MN ⊥ NP.

Vậy: $d(\mathrm{AM},\mathrm{NP})=\mathrm{MN}=\frac{a}{2}$

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: