Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a

Bài 6 trang 86 Toán 11 Tập 2: Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S, BC, A] có số đo là

A. 75°46′.

B. 71°21′.

C. 68°31′.

D. 65°12′.

Trả lời

Đáp án đúng là: D

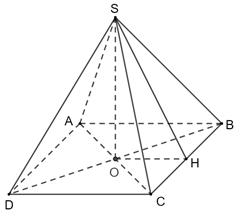
Gọi O là tâm của đáy.

Kẻ OH ⊥ BC (H $\in$ BC)

Vì ΔSAC cân tại S nên SO ⊥ AC.

Vì ΔSBD cân tại S nên SO ⊥ BD.

⇒ SO ⊥ (ABCD) ⇒ SO ⊥ BC.

Mà OH ⊥ BC nên $\widehat{\mathrm{SHO}}$ là góc nhị diện [S, BC, A].

$S_{\mathrm{ABCD}}=\mathrm{AB}.\mathrm{AD}=12a^2\Rightarrow {\text{S}}_{\text{OBC}}=\frac{1}{4}{S}_{\mathrm{ABCD}}=3a^2$.

Mà $S_{\mathrm{OBC}}=\frac{1}{2}.\mathrm{BC}.\mathrm{OH}\Rightarrow \mathrm{OH}=\frac{2S_{\mathrm{OBC}}}{\mathrm{BC}}=2a$.

• $\mathrm{AC}=\sqrt{{\mathrm{AB}}^2+{\mathrm{BC}}^2}=5a\Rightarrow \mathrm{OC}=\frac{1}{2}\mathrm{AC}=\frac{5a}{2}$.

• $\mathrm{SO}=\sqrt{{\mathrm{SC}}^2-{\mathrm{OC}}^2}=\frac{5a\sqrt{3}}{2}$.

• $\tan \widehat{\mathrm{SHO}}=\frac{\mathrm{SO}}{\mathrm{OH}}=\frac{5\sqrt{3}}{4}\Rightarrow \widehat{\mathrm{SHO}}\approx 65°12\text{'}$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: