Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a

Bài 11 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60°. Gọi I là trung điểm của cạnh AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD theo a.

Trả lời

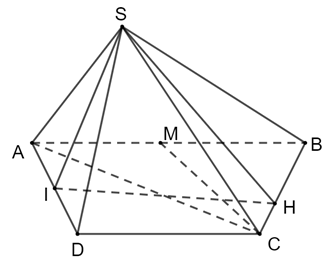
Kẻ IH ⊥ BC

Ta có:

$\left.\begin{array}{l}\left(\mathrm{SIB}\right)\perp \left(\mathrm{ABC}\text{D}\right)\\ \left(\mathrm{SIC}\right)\perp \left(\mathrm{ABC}\text{D}\right)\\ \left(\mathrm{SIB}\right)\cap \left(\mathrm{SIC}\right)=\mathrm{SI}\end{array}\right\}\Rightarrow \mathrm{SI}\perp (ABCD)$

Suy ra: SI ⊥ BC mà BC ⊥ IH ⇒ BC ⊥ (SHI) $\Rightarrow$ BC ⊥ SH.

Lại có: $[S,\mathrm{BC},A]=\widehat{\mathrm{SHI}}=60°$.

$S_{\mathrm{ABC}\text{D}}=\frac{1}{2}\left(\mathrm{AB}+\mathrm{CD}\right)\mathrm{AD}=3a^2$;

Ta có: I là trung điểm AD $\Rightarrow$ $\mathrm{AI}=\mathrm{ID}=\frac{1}{2}\mathrm{AD}=a$.

${\mathrm{S}}_{\mathrm{ABI}}=\frac{1}{2}.\mathrm{AB}.\mathrm{AI}={\mathrm{a}}^2$

${\mathrm{S}}_{\mathrm{I}\text{D}\mathrm{C}}=\frac{1}{2}.\mathrm{CD}.\mathrm{ID}=\frac{{\mathrm{a}}^2}{2}$

${\mathrm{S}}_{\mathrm{IBC}}={\mathrm{S}}_{\mathrm{ABCD}}-{\mathrm{S}}_{\mathrm{AIB}}-{\mathrm{S}}_{\mathrm{CID}}=\frac{3{\text{a}}^2}{2}$

Gọi M là trung điểm của AB.

$\Rightarrow \mathrm{BM}=\frac{1}{2}\mathrm{AB}=a$, CM = AD = 2a $\Rightarrow \mathrm{BC}=\sqrt{{\mathrm{BM}}^2+{\mathrm{CM}}^2}=a\sqrt{5}$ ;

$\Rightarrow \mathrm{IH}=\frac{2S_{\mathrm{IBC}}}{\mathrm{BC}}=\frac{3\text{a}\sqrt{5}}{5}$ $\Rightarrow \mathrm{SI}=\mathrm{IH}.\tan 60°=\frac{3a\sqrt{15}}{5}$.

Vậy $V_{S.\mathrm{ABC}\text{D}}=\frac{1}{3}.\mathrm{SI}.S_{\mathrm{ABC}\text{D}}=\frac{3{\text{a}}^3\sqrt{15}}{5}$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: