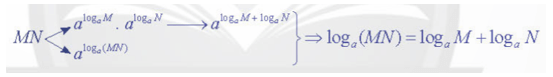Cho các số thực dương a, M, N với a ≠ 1>. Bạn Quân đã vẽ sơ đồ và tìm ra công thức

Hoạt động khám phá 2 trang 16 Toán 11 Tập 2: Cho các số thực dương a, M, N với a ≠ 1>. Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức ${\log }_a\left(MN\right)$ như sau:

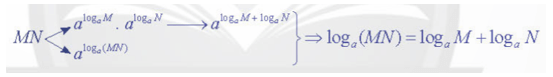
a) Giải thích cách làm của bạn Quân.

b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho ${\log }_a\frac{M}{N}$ và ${\log }_a{M}^{\alpha }\left(\alpha \in ℝ\right)$ .

Trả lời

a) Bạn Quân viết tích MN theo hai cách:

$MN=a^{{\log }_a\left(MN\right)}$ và $MN=a^{{\log }_{a}M+{\log }_{a}N}$.

Suy ra $MN=a^{{\log }_{a}M+{\log }_{a}N}=a^{{\log }_a\left(MN\right)}$.

Từ đó, nhận được ${\log }_a\left(MN\right)={\log }_{a}M+{\log }_{a}N$.

b) Tương tự $\frac{M}{N}=a^{{\log }_a\frac{M}{N}}$ và $\frac{M}{N}=\frac{a^{{\log }_{a}M}}{a^{{\log }_{a}N}}=a^{{\log }_{a}M-{\log }_{a}N}$.

Suy ra $a^{{\log }_a\frac{M}{N}}=a^{{\log }_{a}M-{\log }_{a}N}$.

Từ đó, nhận được ${\log }_a\frac{M}{N}={\log }_{a}M-{\log }_{a}N$.

Tiếp tục, có $M^{\alpha }=a^{\log {}_a{M}^{\alpha }}$ và $M^{\alpha }={\left(a^{\log {}_{a}M}\right)}^{\alpha }=a^{\alpha \log {}_{a}M}$.

Suy ra $a^{\log {}_a{M}^{\alpha }}=a^{\alpha \log {}_{a}M}$.

Từ đó, nhận được ${\log }_a{M}^{\alpha }=\alpha {\log }_{a}M$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: