Cho tam giác ABC có đường trung tuyến AM (M ∈ BC). Tia phân giác của góc AMB  cắt AB tại D, tia phân giác của góc AMC cắt AC tại E

Bài 6 trang 48 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có đường trung tuyến AM (M ∈ BC). Tia phân giác của $\widehat{AMB}$ cắt AB tại D, tia phân giác của $\widehat{AMC}$ cắt AC tại E.

a) Chứng minh DE // BC;

b) Gọi I là giao điểm của DE với AM. Chứng mình I là trung điểm của DE.

Trả lời

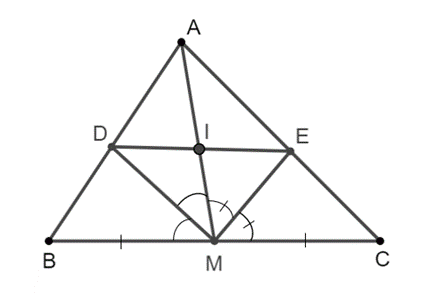
Vì ME là phân giác của $\widehat{AMC}$ trong ∆ABC nên $\frac{EA}{EC}=\frac{MA}{MC}$.

Mà MB = MC, suy ra $\frac{DA}{DB}=\frac{EA}{EC}$.

Xét ∆ABC có $\frac{DA}{DB}=\frac{EA}{EC}$ nên theo định lí Thalès đảo, ta có DE // BC.

b) Theo hệ quả của định lí Thalès:

• Xét ∆ABM có DI // MB (vì I ∈ DE, M ∈ BC), ta có $\frac{AI}{AM}=\frac{DI}{MB}$.

• Xét ∆ACM có EI // MC, ta có $\frac{AI}{AM}=\frac{IE}{MC}$.

Suy ra $\frac{IE}{MC}=\frac{DI}{MB}$, mà MC = MB, suy ra IE = DI.

Vậy I là trung điểm của DE.

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Định lí Thalès trong tam giác

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7

Bài 1: Hai tam giác đồng dạng

Bài 2: Các trường hợp đồng dạng của hai tam giác