Cho tam giác ABC nhọn có các đường cao BD,CE. Tia phân giác của các góc ACE,ABD cắt nhau tại O và cắt AB,AC lần lượt tại M,N

Bài 28 trang 100 SBT Toán 8 Tập 1: Cho tam giác $ABC$ nhọn có các đường cao $BD,CE$. Tia phân giác của các góc $ACE,ABD$ cắt nhau tại $O$ và cắt $AB,AC$ lần lượt tại $M,N$. Tia $BN$ cắt $CE$ tại $K$, tia $CM$ cắt $BD$ tại $H$. Chứng minh:

a) $BN\mathrm{\perp }CM$

b) Tứ giác $MNHK$ là hình thoi.

Trả lời

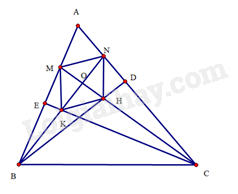
a) Do tam giác $ABD$ vuông tại $D$ và tam giác $ACE$ vuông tại $E$ nên $\widehat{ABD}+\hat{A}=\widehat{ACE}+\hat{A}={90}^{\circ }$. Suy ra $\widehat{ABD}=\widehat{ACE}$.

Mà $BN$ và $CM$ lần lượt là tia phân giác của $\widehat{ABD}$ và $\widehat{ACE}$, suy ra $\widehat{ABN}=\widehat{DBN}=\widehat{ACM}=\widehat{ECM}$.

Do tam giác $CEM$ vuông tại $E$ nên $\widehat{ECM}+\widehat{EMC}={90}^{\circ }$

Suy ra $\widehat{ABN}+\widehat{EMC}={90}^{\circ }$ hay $\widehat{MBO}+\widehat{BMO}={90}^{\circ }$.

Do đó ta tính được $\widehat{BOM}={90}^{\circ }$. Vậy $BN\mathrm{\perp }CM$.

b)  $\mathrm{\Delta }BMO=\mathrm{\Delta }BHO$ (cạnh góc vuông – góc nhọn kề). Suy ra $OM=OH$

$\mathrm{\Delta }CNO=\mathrm{\Delta }CKO$ (cạnh góc vuông – góc nhọn kề). Suy ra $ON=OK$.

Tứ giác $MNHK$ có hai đường chéo $MH$ và $NK$ cắt nhau tại trung điểm $O$ của mỗi đường nên $MNHK$ là hình bình hành.

Hình bình hành $MNHK$ có $MH\mathrm{\perp }NK$ nên $MNHK$ là hình thoi.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài tập cuối chương 5 trang 103